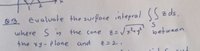NEED HELP :/
- Thread starter reis
- Start date
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
Hello reis. Did you start the exercise? Tutors would like to know where you got stuck. If you have any specific questions about the exercise, please post them also.
We ask new members to read the forum's posting guidelines. Thank you!
\(\;\)
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Where are you stuck? They told you what the integrand z equals in terms of x and y, so that can't be the trouble. Did you find the limits? Do you know how to integrate z? This is a help site and it is extremely hard to help you if you don't tell us where you need help. Please post back showing us your work.
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
If \(\displaystyle z= \sqrt{x^2+ y^2}\) the \(\displaystyle z^2= x^2+ y^2\). A standard parameterization for something involving \(\displaystyle x^2+ y^2\) is \(\displaystyle x= r\cos(\theta)\), \(\displaystyle y= r\sin(\theta)\) because then \(\displaystyle z= x^2+ y^2= r^2 \cos^2(\theta)+ r^2\sin^2(\theta)= r^2\). We can write the surface as the vector equation \(\displaystyle x\vec{i}+ y\vec{j}+ z\vec{k}= r\cos(\theta)\vec{i}+ r\sin(\theta)\vec{j}+ r^2\vec{k}\).
The derivative of that with respect to r is \(\displaystyle \cos(\theta)\vec{i}+ \sin(\theta)\vec{j}+ 2r\vec{k}\). The derivative with respect to \(\displaystyle \theta\) is \(\displaystyle -r\sin(\theta)\vec{i}+ r\cos(\theta)\vec{j}\). The vector differential of surface area, normal to the surface and with length the surface area differential is given by the cross product of those two vectors:
\(\displaystyle \left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-r\sin(\theta) & r\cos(\theta) & 0 \\ \cos(\theta) & \sin(\theta) & 2r \end{array}\right|= 2r\cos(\theta)\vec{i}+ 2r\sin(\theta)\vec{j}+ r^2\vec{k}\)
The derivative of that with respect to r is \(\displaystyle \cos(\theta)\vec{i}+ \sin(\theta)\vec{j}+ 2r\vec{k}\). The derivative with respect to \(\displaystyle \theta\) is \(\displaystyle -r\sin(\theta)\vec{i}+ r\cos(\theta)\vec{j}\). The vector differential of surface area, normal to the surface and with length the surface area differential is given by the cross product of those two vectors:
\(\displaystyle \left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-r\sin(\theta) & r\cos(\theta) & 0 \\ \cos(\theta) & \sin(\theta) & 2r \end{array}\right|= 2r\cos(\theta)\vec{i}+ 2r\sin(\theta)\vec{j}+ r^2\vec{k}\)