Need help understanding Calculating a specific coefficient or term

[thickmax]

I have an example worked through, but i do not know how a number is being calculated...

Calculating a specific coefficient or term
The formula is particularly effective when you have to calculate a specific coefficient or term in an expansion

For example you may be asked to calculate e.g. the coefficient of x⁴ in (3+2x)¹⁵.

Pascal's Triangle would clearly be an inefficient way of doing this as you would have to calculate all the rows down to the fifteenth.

Expanding the whole expression would also be inefficient. We only need the x4 term so why would we calculate all of the 14 other terms too?

The term that contains the x⁴ is calculated by

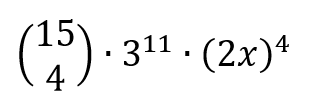
So the term containing x⁴ is 1365×177147×16x⁴=3868890480x⁴


Where does the 1365 come from?

Please could someone show me the steps to calculating it?

 

[Dr.Peterson]

The term that contains the x4 is calculated by

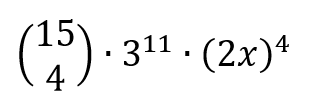
So the term containing x4 is 1365×177147×16x4=3868890480x4


Where does the 1365 come from?

Please could someone show me the steps to calculating it?

Have you learned the binomial theorem, which this is about? The notation (called the binomial coefficient) means

[MATH]{15\choose 4}=\frac{15!}{4!(15-4)!}=\frac{15\cdot14\cdot13\cdot12}{4\cdot3\cdot2\cdot1}=\frac{32760}{24}=1365[/MATH]​

 

[pka]

SEE HERE

 

[JeffM]

Your question is odd. Presumably this comes from a discussion of the binomial theorem.

[MATH](a + b)^n = \sum_{j=0}^n \dbinom{n}{j} * a^{(n-j)} * b^j, \text { where } \dbinom{n}{j} = \dfrac{n!}{j! * (n - j)!}.[/MATH]
That sum has n + 1 terms.

In your problem, a = 3 and b = 2x. And j = 4 while n = 15. This is pure plug and chug. Perhaps you were confused because one of the variables was equal to a constant, namely 3.

 

[Steven G]

There are three factors in the formula and three numbers being multiplied. The first factor, the one you are asking about, comes from the 1st factor which is 1365. That number will be the 5th entry of the 15th row of pascal's triangle.

 

[thickmax]

Your question is odd. Presumably this comes from a discussion of the binomial theorem.

[MATH](a + b)^n = \sum_{j=0}^n \dbinom{n}{j} * a^{(n-j)} * b^j, \text { where } \dbinom{n}{j} = \dfrac{n!}{j! * (n - j)!}.[/MATH]
That sum has n + 1 terms.

In your problem, a = 3 and b = 2x. And j = 4 while n = 15. This is pure plug and chug. Perhaps you were confused because one of the variables was equal to a constant, namely 3.

Plugged and Chugged, thanks for the explanation, the example didn't have every step which after just learning the process, was overlooked by me