my set up #2

[Ryan Rigdon]

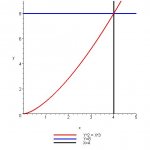
i cant for the love of god figure why these type of problems are giving me so much trouble. i have three problems left that deal with disk, shell, and washer. here is my next problem. would just like to know if my set up is write before i continue with them. if someone could make sure their right would greatly be appreciated. thank you.

 

[wjm11]

Region bounded by y^2 = x^3, x = 4, and the x-axis.

Rotate about x = 4:
Part A looks fine, except I’d use x^1.5 or x^(3/2) rather than x(sqrt(x)).

Rotate about y = 8:
For B, you want A = pi(R^2 – r^2) = pi(8^2 – (x^1.5)^2) = pi(64 – x^3).
So deltaV = pi(64 – x^3)dx

 

[Ryan Rigdon]

i will give your hints a shot then post my work. thanx.

 

[tkhunny]

"A" is excellent. Tell me why you get to keep only half the function when you solve for 'y'.

OR


\(\displaystyle \int_{0}^{8}\pi \left(4-y^{\frac{2}{3}}\right)^{2}\;dy\)

The very best way I know to check your work is to solve it two ways and achieve the same, unique result.

 

[BigGlenntheHeavy]

\(\displaystyle A. \ Revolved \ around \ x \ = \ 4\)

\(\displaystyle Disc: \ \pi\int_{0}^{8}(4-y^{2/3})^2dy \ = \ \frac{1024\pi}{35}\)

\(\displaystyle Shell: \ 2\pi\int_{0}^{4}(4-x)x^{3/2}dx \ = \ \frac{1024\pi}{35}\)

\(\displaystyle B. \ Revolved \ around \ y \ = \ 8\)

\(\displaystyle Disc: \ \pi\int_{0}^{4}[(0-8)^2-(x^{3/2}-8)^2]dx \ = \ \frac{704\pi}{5}\)

\(\displaystyle Shells: \ 2\pi\int_{0}^{8}(8-y)(4-y^{2/3})dy \ = \ \frac{704\pi}{5}\)

\(\displaystyle See \ graph\)

[attachment=0:17be81dn]III.jpg[/attachment:17be81dn]

 

[tkhunny]

For "B", are you sure we're doing the right piece?

 

[Ryan Rigdon]

sorry it took so long to reply. but i wanted to make sure i totally understand the problem. for part B i forgot to put a line in for y = 8. so here are my results. by the way they equal yours BigGlenntheHeavy. Now its on to the next problem. only two to go.