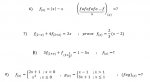[MOVED] Please help me in resolve these "function" problems

[jpmo02]

HelloCan you help me in any these questions ?Please help me to solve this math problems!the question's is on the attachment files. (attach is fieled!)http://oi58.tinypic.com/2afzqt2.jpghttp://oi62.tinypic.com/b9afie.jpgThanks

 

[Deleted member 4993]

HelloCan you help me in any these questions ?Please help me to solve this math problems!the question's is on the attachment files. (attach is fieled!)http://oi58.tinypic.com/2afzqt2.jpghttp://oi62.tinypic.com/b9afie.jpgThanks

Most of us are not willing to go to another website to retrieve problems. Please copy and paste (or type it up) and post here.

 

[jpmo02]

Please check the attachment files.
and
Please help me ...
Thanks

 

[Deleted member 4993]

Please check the attachment files.
and
Please help me ...
Thanks

What are your thoughts?

If you are stuck at the beginning tell us and we'll start with the definitions.

Please share your work with us ... even if you know it is wrong

You need to read the rules of this forum. Please read the post titled "Read before Posting" at the following URL:

http://www.freemathhelp.com/forum/th...Before-Posting

 

[stapel]

Please help me

1. Given that \(\displaystyle f\) is a linear function and that \(\displaystyle \, f\, \circ\, f_{(x)}\, =\, 4x\, +\, 3, \,\) find \(\displaystyle f_{(x)}.\)

What techniques have they taught you for this? You have been given that f(x) = mx + b for some values of m and b. So you plugged this into the composition of functions that is indicated, set this equal to the result, and... then what?

By the way, would it be correct for us to assume that "\(\displaystyle f_{(x)}\)" means "\(\displaystyle f(x)\)"? If so, please confirm; if not, please provide whatever definition you've been given for this notation. Thank you!

2. Given that \(\displaystyle \, f_{(x)}\, =\, \sqrt{-x^2\, -\, 3x\, +\, 4\,}\,\) and \(\displaystyle \, g_{(x)}\, =\, f_{(x^2\, +\, x\, +\, 1)},\, \) find \(\displaystyle D_g.\)

Does "\(\displaystyle g_{(x)}\, =\, f_{(x^2\, +\, x\, +\, 1)},\)" mean that the formula for \(\displaystyle g(x)\) is given by the result when you plug \(\displaystyle x^2\, +\, x\, +\, 1\) into \(\displaystyle f(x)\)? Also, what is the meaning of \(\displaystyle D_g\)?

3. Given that \(\displaystyle \,f_{\left(\dfrac{x^4\, -\, 1}{x^4\, +\, 1}\right)}\, =\, x^4\, +\, x^8\, +\, x^16,\,\) find \(\displaystyle \,f_{\left(\dfrac{1}{2}\right)}.\)

How far have you gotten in figuring out an x-value which will give you 1/2 when you plug it in for x in (x⁴ - 1)/(x⁴ + 1)?

4. Given that \(\displaystyle \,f_{(x)}\, =\, \sqrt{x\,}\,\) and \(\displaystyle \,g_{(x)}\, =\, \dfrac{2\, -\, x}{1\, +\, x},\,\) find \(\displaystyle \,R_{g\, \circ\, f}.\)

What is the definition of \(\displaystyle R_{g}\)?

5. Given that \(\displaystyle \, f_{\left(\dfrac{x}{x^2\, +\, x\, +\, 1}\right)}\, =\, \dfrac{x^2}{x^4\, +\, x^2\, +\, 1},\,\) find \(\displaystyle \, f_{(x)}.\)

6. Given that \(\displaystyle \, f_{(x)}\, =\, \left|\, x\, \right|\, -\, x,\, \) find \(\displaystyle \, \left(\underbrace{f\, \circ\, f\, \circ\, f\, \circ\, f\, \circ\, ... \, \circ\, f}_\text{n times}\right).\)

7. Given that \(\displaystyle \, f_{(2\, -\, x)}\, +\, 4\, f_{(2\, +\, x)}\, =\, 2x,\, \) prove that \(\displaystyle \, f_{(x)}\, =\, \left(\dfrac{2}{3}\right)(x\, -\, 2).\)

8. Given that \(\displaystyle \, 3\, f_{(1\, +\, x)}\, +\, f_{\left(1\, +\, \dfrac{1}{x}\right)}\, =\, 1\, -\, 5x,\, \) find \(\displaystyle \, f_{(x)}.\)

9. Given that \(\displaystyle \, f_{(x)}\, =\, \begin{cases}2x\, +\, 1&\mbox{ for }& x\, >\, 0\\x^2&\mbox{ for }&x\, \leq\, 0\end{cases}\, \) and \(\displaystyle \, g_{(x)}\, =\, \begin{cases}x\, -\, 1&\mbox{ for }& x\, >\, 1\\3x\, +\, 1&\mbox{ for }&x\, \leq \, 1\end{cases},\, \) find \(\displaystyle \, \left(f\, \circ \, g\right)_{(x)}.\)

What have you tried for these? What are your thoughts? Please be complete. Thank you!