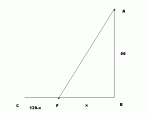
I'm not exactly sure, as I just don't know how to do it, but it probably concerns finding a formula to describe cost, then finding dy/dx = 0 to find the minimum. The reason I've shown no working, is that I don't know where to start exactly. If I could find a formula I'm sure I could do the rest, but I'm not sure where to go at the moment.
Please help
Please help