
So I have that. and I make this diagram, getting in rads the angle with arcsin(100/200)
This is my diagram of what I think is going on.
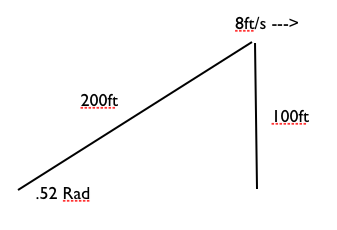
I also get 100^2 + x^2 = 200^2 as the forumla for the base of the triangle but I don't quite get how to find the rate of change. These are really weirding me out as each word problem is about something else and I don't know how to apply the concept to each one.
