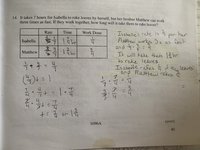
This is the last word problem on my test that I can’t figure out. I have an example from my book with a similar problem but the missing numbers are switched so it doesn’t actually help me to solve it. So far I know that if Isabella takes 7 hours to rake leaves on her own and her brother is 3 times as fast, he takes 2 1/3 hr to rake leaves on his own. So following my book’s example, she rakes leaves at a rate of 1/3t and he rakes leaves at a rate of 1/t. But, I don’t know what to do after this. (You can see some of my notes trying to figure this out on the answer sheet for my practice questions but I have way more elsewhere and still was confused)
More help needed with rational equations
- Thread starter kathrynk
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
The example you show is a harder type of problem, in which the unknown is the time it takes a person to do a job alone.
In your problem, you know the rates alone; Isabella does 1/7 of the job per hour, and Matthew's rate is 3 times that. No variable is needed there. The unknown is how long it takes together. (Commonly you would have been given an example like this first, before the example you showed.)
The unknown goes in the middle column, the time taken when they work together.
In your problem, you know the rates alone; Isabella does 1/7 of the job per hour, and Matthew's rate is 3 times that. No variable is needed there. The unknown is how long it takes together. (Commonly you would have been given an example like this first, before the example you showed.)
The unknown goes in the middle column, the time taken when they work together.
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
"she rakes leaves at a rate of 1/3t and he rakes leaves at a rate of 1/t" doesn't make sense because you haven't said what "t" represents. If Isabella takes 7 hours to rake leaves (from 1 lawn, say) she rakes leaves at a rate of 1/7 lawn per hour. If her brother, working three times as fast, rakes a yard in 7/3 hours then he rakes 3/7 yard per hour. Working together their rates add so they work at 1/7+ 3/7= 4/7 yard per hour and so take 7/4= 1.75 hours to rake the lawn.
Yes I understood that from the example given in my book. So I want to add up to 7/7. From Hall of Ivy’s post I realize they work at a rate of 4/7 an hour but I’m confused how inverting to 7/4 helps. Or how to figure out how much of an hour 3/7 of the yard takes. Or how much each of them does individually for the third column
I’m sorry I wrote it like that. That was me going by the example from the text book and making things more complicated for myself adding in t (Time to complete the task on their own) when I already know what it is. But I still don’t totally understand the end of your answer? Why would I invert 7/4 to get the total time?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
The goal is to find "hours per lawn" -- how long it takes. That is the reciprocal of "lawns per hour" -- how fast you work.
This kind of problem is all about this reciprocal relationship. In fact, that's why these problems are taught as part of studying rational equations!
This kind of problem is all about this reciprocal relationship. In fact, that's why these problems are taught as part of studying rational equations!
Okay doing it reciprocally(?) does in fact translate to 7/4 like hall of ivy said or 1 3/4 hours. And now I have to find what they each contributed to that time and I think I can figure that out since that is shown in the answer key for the example. I jsut have to use the LCD bc it won’t translate from sevenths to fourths otherwise
Yes? He works 3 times as fast as she does. So even tho the denominator/time frame is different, if out of 1 3/4 hours she works 1/4, 1/4 x 3 is 3/4s so it adds up to a whole while considering their individual rates.