methods of volume region setup work shown need help!

[johnq2k7]

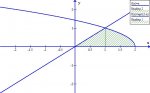
Indicate the method you use to set up the integrals (do not integrate) that give the volume of the solid generated by rotating the region R around:

The region R is bounded by the curves y=x, x= 2-y^2 and y=0

i.) the x-axis
ii.) the y-axis
iii.) the line x= -2
iv.) the line y= 1

work shown:

y=x ,

x= 2- y^2
y= sqrt(2-x)

i.) integral of Pi*[(x)- (sqrt(2-x))] dx as x goes from 0 to 1 (Washer Method)

ii.) integral of 2*Pi*x*[(x)-sqrt(2-x)]dx as y goes from 0 to 1 (Shell Method)

iii.) integral of 2*Pi*(-2-x)*[(x)-(sqrt(2-x))]dx as x goes from 0 to 1 (Shell Method)

iv.) integral of Pi*[(x-1)-(sqrt(2-x-1)]dx as y goes from 0 to 1 (Washer Method)

I think my definite integral limits are wrong... and in general my integral setup is wrong.. please help

 

[galactus]

The region R is bounded by the curves $\displaystyle y=x, \;\ x= 2-y^{2} \;\ and \;\ y=0$

If I am interpreting correctly, the problem says it is bounded by y=0. Look at the region. The limits would then be 0 to 2.

i.) the x-axis

$\displaystyle {\pi}\int_{0}^{2}[x^{2}+x-2]dx$

ii.) the y-axis

$\displaystyle 2{\pi}\int_{0}^{2}x(x-\sqrt{2-x})dx$

iii.) the line x= -2

$\displaystyle 2{\pi}\int_{0}^{2}(x+2)(x-\sqrt{2-x})dx$

iv.) the line y= 1

$\displaystyle {\pi}\int_{0}^{2}(x^{2}-x-2+2\sqrt{2-x})dx$