JulianMathHelp
Junior Member
- Joined
- Mar 26, 2020
- Messages
- 160
Multiple Choice: Jamila has started to construct a line parallel to line m through point Q at right. Which of the possible strategies below make the most sense to help her find the line parallel to m through point Q?
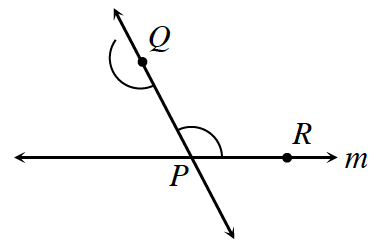
What does it mean to measure the arc centered at P? How do you measure the arc? Can someone explain B to me?

- Measure ∠QPR with a protractor.
- Use the compass to measure the arc centered at P, then place the point of the compass where the arc centered at Q meets QP¯, and mark that measure off on the arc.
- Construct QR¯.
- Measure PR with a ruler.
What does it mean to measure the arc centered at P? How do you measure the arc? Can someone explain B to me?


