Maximum Area...
- Thread starter rafeeki92
- Start date
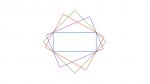
[attachment=0:2spvet6b]rectangles.jpg[/attachment:2spvet6b]Geometrically speaking......
Draw your rectangle.
Draw a square with sides at 45 degrees to the rectangle touching the rectangle corners.
This square encloses the rectangle.
Now draw any other rectangle circumscribing your rectangle.
This rectangle is a smaller one as you rotate the external square to approach the area of
your original rectangle.
I'm not sure if I worded that clearly.
Let's say the rectangle at 45 degrees (it's a square) is green.
Your original one is blue.
The one you drew in between them is red.
Imagine turning the green one and shrinking it until it becomes the blue one.
The red one is one that the green one shrunk to on it's way to merging into the blue one.
So the red one's area is less than the green outer one's area.
So the green one has maximum area.
You can get it's dimensions from trigonometry or Pythagoras' theorem.
However, it's simplest to look at it in terms of triangle areas.
The triangles of the square have greater area (0.5base(height))
than the triangles of any other circumscribing rectangle.
Draw your rectangle.
Draw a square with sides at 45 degrees to the rectangle touching the rectangle corners.
This square encloses the rectangle.
Now draw any other rectangle circumscribing your rectangle.
This rectangle is a smaller one as you rotate the external square to approach the area of
your original rectangle.
I'm not sure if I worded that clearly.
Let's say the rectangle at 45 degrees (it's a square) is green.
Your original one is blue.
The one you drew in between them is red.
Imagine turning the green one and shrinking it until it becomes the blue one.
The red one is one that the green one shrunk to on it's way to merging into the blue one.
So the red one's area is less than the green outer one's area.
So the green one has maximum area.
You can get it's dimensions from trigonometry or Pythagoras' theorem.
However, it's simplest to look at it in terms of triangle areas.
The triangles of the square have greater area (0.5base(height))
than the triangles of any other circumscribing rectangle.
Attachments
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Max. \ Area \ of \ rectangle \ circumscribed \ around \ rectangle \ with \ length \ = \ L \ and \ width \ = \ W,\)
\(\displaystyle is \ 2LW. \ See \ Chrism \ graph, \ simple \ algebra \ will \ give \ you \ the \ answer.\)
\(\displaystyle Question: \ What \ is \ the \ Area \ of \ the \ square \ circumscribed \ about \ the \ rectangle \ with \ length \ L \ and\)
\(\displaystyle width \ W \ in \ L \ and \ W \ terms.\?\)
\(\displaystyle is \ 2LW. \ See \ Chrism \ graph, \ simple \ algebra \ will \ give \ you \ the \ answer.\)
\(\displaystyle Question: \ What \ is \ the \ Area \ of \ the \ square \ circumscribed \ about \ the \ rectangle \ with \ length \ L \ and\)
\(\displaystyle width \ W \ in \ L \ and \ W \ terms.\?\)
BigGlenntheHeavy
Senior Member
- Joined
- Mar 8, 2009
- Messages
- 1,577
\(\displaystyle Afterthought: \ If \ memory \ serves \ me \ correct, \ the \ max. \ area \ of \ any \ quadrilateral \ circumscribed\)
\(\displaystyle about \ a \ rectangle \ with \ length \ L \ and \ width \ W \ is \ a \ square \ whose \ area \ is \ LW+L^{2}/2+W^{2}/2.\)
\(\displaystyle All \ rectangles, \ ignoring \ the \ trivial \ case, \ circumscribed \ about \ said \ rectangle, \ all \ have \ the \ same\)
\(\displaystyle area, \ to \ wit: \ A \ = \ 2LW, \ the \ square \ occurs \ when \ the \ line \ tangent \ to \ a \ corner \ = \ 45^{0}.\)
\(\displaystyle Liked \ I \ said, \ if \ memory \ serves \ me \ correct.\)
\(\displaystyle about \ a \ rectangle \ with \ length \ L \ and \ width \ W \ is \ a \ square \ whose \ area \ is \ LW+L^{2}/2+W^{2}/2.\)
\(\displaystyle All \ rectangles, \ ignoring \ the \ trivial \ case, \ circumscribed \ about \ said \ rectangle, \ all \ have \ the \ same\)
\(\displaystyle area, \ to \ wit: \ A \ = \ 2LW, \ the \ square \ occurs \ when \ the \ line \ tangent \ to \ a \ corner \ = \ 45^{0}.\)
\(\displaystyle Liked \ I \ said, \ if \ memory \ serves \ me \ correct.\)
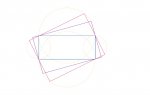
[attachment=0:2xr8l6me]rectangles2.jpg[/attachment:2xr8l6me]
Yes,
the green-bordered triangle standing on top of the blue rectangle has greatest area,
among all the right-angled triangles whose hypotenuse rests on top of the blue rectangle.
It's area is 0.5(L)(L/2).
Same story for the triangles underneath the blue rectangle.
For those at the sides, the green-bordered one has area 0.5(W)(W/2).
The remaining area of the green square is the blue rectangle area.
Total area = 2(0.5)(L[sup:2xr8l6me]2[/sup:2xr8l6me]/2)+2(0.5)(W[sup:2xr8l6me]2[/sup:2xr8l6me]/2)+LW.
Alternatively, we could try to calculate the width and length of a circumscribing rectangle,
by calculating the chord lengths in the semicircles and solving for maximum product of rectangle sides.
This is far more work than noticing that all right-angled triangles within the semicircles have the same base,
therefore the one with maximum height has greatest area.
This happens when the circumscribing rectangle is a square.
Yes,
the green-bordered triangle standing on top of the blue rectangle has greatest area,
among all the right-angled triangles whose hypotenuse rests on top of the blue rectangle.
It's area is 0.5(L)(L/2).
Same story for the triangles underneath the blue rectangle.
For those at the sides, the green-bordered one has area 0.5(W)(W/2).
The remaining area of the green square is the blue rectangle area.
Total area = 2(0.5)(L[sup:2xr8l6me]2[/sup:2xr8l6me]/2)+2(0.5)(W[sup:2xr8l6me]2[/sup:2xr8l6me]/2)+LW.
Alternatively, we could try to calculate the width and length of a circumscribing rectangle,
by calculating the chord lengths in the semicircles and solving for maximum product of rectangle sides.
This is far more work than noticing that all right-angled triangles within the semicircles have the same base,
therefore the one with maximum height has greatest area.
This happens when the circumscribing rectangle is a square.
