Maximizing area of a trapezoid

[Funkychemist]

Hey guys I'm having a problem with, well, a problem.

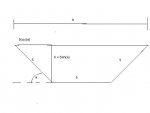
The cross-section of a drain is a trapezoid. The sides and the bottom of the trapezoid each have a length of 5 feet. Determine the angle $\displaystyle \theta$ such that the drain will have maximal cross-sectional area.

So far, I have used the area of a trapezoid formula and substituted 5sin$\displaystyle \theta$ in for h and proceeded to take the derivative of the area with respect to $\displaystyle \theta$ and set it equal to 0. However, I get $\displaystyle 0 = 25cos\theta$ which would make $\displaystyle \theta = 90$. Can anyone give me a push in the right direction?

 

[mmm4444bot]

You did not define theta, but from your reasoning it appears that theta is the angle where the sides meet the top. Is this the angle for which the exericse asks?

Using 5 sin(?) for the height, I get the following expression for the area:

25 sin(?) [cos(?) + 1]

This function has a local maximum such that 0 < ? < Pi/2 .

 

[Funkychemist]

All that was given in the problem was exactly what I wrote, no diagram to go with it. Could you provide an explanation as to where the cos$\displaystyle \theta$ + 1 came from?

 

[mmm4444bot]

Since nobody told you which of the trapezoid's interior angles is theta, did you arbitrarily assign theta to the angle at the top?

Using your choice of theta, the height is 5 sin(?).

Therefore, the length of the top is 5 cos(?) + 5 + 5 cos(?).

The area formula for a trapezoid contains a factor which is the average of the top and bottom.

The average of the top and bottom is [5 cos(?) + 5 + 5 cos(?) + 5]/2.

This expression simplifies to 5 [cos(?) + 1].

That's from where the factor cos(?) + 1 comes.

 

[Funkychemist]

Ok I think I got that, last question (I think). I understand where cos$\displaystyle \theta$ + 1 came from; however, why is that multiplied by 25 sin$\displaystyle \theta$ to get the area equation? I'm probably over-thinking this, but 8 hours of calculus will do that to you :lol:

 

[mmm4444bot]

why is [cos(?) + 1] multiplied by 25 sin$\displaystyle \theta$ to get the area

The average of the bases is 5[cos(?) + 1].

The height is 5 sin(?).

The area is the product of this average and the height.

What formula do you have for the area of a trapezoid?

 

[Funkychemist]

The formula I was using was $\displaystyle A = \frac{h}{2}(a + b)$.

 

[mmm4444bot]

That's the correct formula.

We can factor it as: h * (a + b)/2

(a + b)/2 is the average of the bases.

This shows that the area of a trapezoid is the product of the base-average times the height.

(a + b)/2 is 5[cos(?) + 1]

h is 5 sin(?)

Their product is 25 sin(?) [cos(?) + 1]

Can you differentiate this expression?

 

[Funkychemist]

The first derivative should be $\displaystyle 25cos^2(\theta) - 25sin^2(\theta) + 25cos(\theta)$. Set that equal to 0 and solve for theta to find a maximum correct? Also, I have a question on another problem, mind if I pm you?

 

[mmm4444bot]

The first derivative should be $\displaystyle 25cos^2(\theta) - 25sin^2(\theta) + 25cos(\theta)$. Set that equal to 0 and solve for theta to find a maximum correct?

Yes, that is correct. I suggest that you find and report both angles (top and bottom) because we don't really know which of these theta is supposed to be.

I prefer that you post your questions on the boards. Please start a new thread for each exercise.

 

[Funkychemist]

So I've gotten as far as $\displaystyle cos(2\theta) + cos(\theta) = 0$, but can't seem to get anything between 0 and $\displaystyle \frac{pi}{2}$ that will give me a value of zero...

Can't perform simple trig, I think it's time for a break.

 

[mmm4444bot]

If you substitute 1 - cos(?)^2 for sin(?)^2 as your first step, you will get an equation that is Quadratic in form.

Letting x = cos(?) leads to 2x^2 + x - 1 = 0

 

[BigGlenntheHeavy]

[attachment=0:1kx1r0al]aaa.JPG[/attachment:1kx1r0al]

This is what I think you want. Can you take it from here?

$\displaystyle Note: \ I \ used \ a \ for \ \theta \ and \ excuse \ the \ drawing \ as \ it \ isn't \ to \ scale.$

 

[Funkychemist]

Assuming I did this correct, I got $\displaystyle \theta = 90$ and $\displaystyle \theta = 60$. Can anyone confirm?

 

[mmm4444bot]

Theta must be between 0 degrees and 90 degrees.

60 degrees is correct.