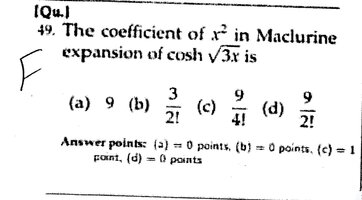YehiaMedhat
Junior Member
- Joined
- Oct 9, 2022
- Messages
- 74
The question is: The coeffiecient of [imath]x^2[/imath] in Maclurine expansion of [imath]cosh(\sqrt{3x})[/imath] is ...
So, trying to solve the question I have to diffrentiate, don't I? so, the first deriviative is [imath]\frac {3sinh(\sqrt{3x})}{2\sqrt{3x}}[/imath], and as it's Maclurine expansion how would I insert the value of x=0 to the deriviative? Is there's a mistake I have done?
So, trying to solve the question I have to diffrentiate, don't I? so, the first deriviative is [imath]\frac {3sinh(\sqrt{3x})}{2\sqrt{3x}}[/imath], and as it's Maclurine expansion how would I insert the value of x=0 to the deriviative? Is there's a mistake I have done?