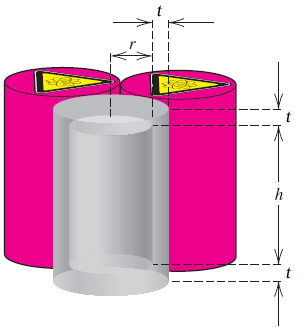
The question is A cylindrical container for storing radioactive waste is to be constructed from lead. This container must be 6 in thick. The volume of the outside cylinder shown in the future is to be 16pi ft3.
a.) Express the height h of the inside cylinder as a function of the inside radius r. (The answer is h=16/(r+0.5)2 -1 but I need to know how to get there)
B.) Show that the inside volume V(r) is given by V(r)= pi r2 (16/(r+0.5)2 -1) (The answer is V(r)=pi r2 h, but need to know the process to find the answer)
Thank you!! I need by tomorrow morning by the way
