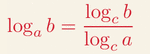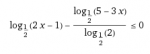Trzewikodziobowna
New member
- Joined
- May 29, 2018
- Messages
- 2
Hello. I am trying to tackle this inequality:
. . . . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_2(5\, -\, 3x)\, \leq\, 0\)
First, find the domain for each of the logs:
. . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1):\)
. . . . .\(\displaystyle 2x\, -\, 1\, >\, 0\)
. . . . .\(\displaystyle x\, >\, \dfrac{1}{2}\)
. . .\(\displaystyle \log_2(5\, -\, 3x):\)
. . . . .\(\displaystyle 5\, -\, 3x\, >\, 0\)
. . . . .\(\displaystyle x\, <\, \dfrac{5}{3}\)
Then should I get rid of the log, by changing the base of 2nd log to 1/2?
. . . . .\(\displaystyle \log_a(b)\, =\, \dfrac{\log_c(b)}{\log_c(a)}\)
. . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_2(5\, -\, 3x)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \dfrac{\log_{\frac{1}{2}}(5\, -\, 3x)}{\log_{\frac{1}{2}}(2)}\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_{\frac{1}{2}}(5\, -\, 3x)\, -\, \log_{\frac{1}{2}}(2)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 2x\, -\, 2\, -\, (5\, -\, 3x\, -\, 2)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 2x\, -\, 1\, -\, 5\, +\, 2x\, +\, 2\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 5x\, -\, 4\, \leq\, 0,\, \Rightarrow\, x\, \leq\, \dfrac{5}{4}\)

is this right?
ed. ah mistake, after leaving logs I should've changed ≤ to ≥ since the base was smaller than 1
. . . . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_2(5\, -\, 3x)\, \leq\, 0\)
First, find the domain for each of the logs:
. . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1):\)
. . . . .\(\displaystyle 2x\, -\, 1\, >\, 0\)
. . . . .\(\displaystyle x\, >\, \dfrac{1}{2}\)
. . .\(\displaystyle \log_2(5\, -\, 3x):\)
. . . . .\(\displaystyle 5\, -\, 3x\, >\, 0\)
. . . . .\(\displaystyle x\, <\, \dfrac{5}{3}\)
Then should I get rid of the log, by changing the base of 2nd log to 1/2?
. . . . .\(\displaystyle \log_a(b)\, =\, \dfrac{\log_c(b)}{\log_c(a)}\)
. . .\(\displaystyle \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_2(5\, -\, 3x)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \dfrac{\log_{\frac{1}{2}}(5\, -\, 3x)}{\log_{\frac{1}{2}}(2)}\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, \log_{\frac{1}{2}}(2x\, -\, 1)\, -\, \log_{\frac{1}{2}}(5\, -\, 3x)\, -\, \log_{\frac{1}{2}}(2)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 2x\, -\, 2\, -\, (5\, -\, 3x\, -\, 2)\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 2x\, -\, 1\, -\, 5\, +\, 2x\, +\, 2\, \leq\, 0\)
. . . . .\(\displaystyle \Rightarrow\, 5x\, -\, 4\, \leq\, 0,\, \Rightarrow\, x\, \leq\, \dfrac{5}{4}\)

is this right?
ed. ah mistake, after leaving logs I should've changed ≤ to ≥ since the base was smaller than 1
Attachments
Last edited by a moderator: