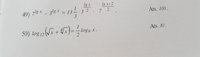Logarithmic Equation
- Thread starter Madcode95
- Start date
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Yes, we can help you!
I suspect that you did not read our guidelines which state that you have to show us your work and state where you are stuck. In this way we know exactly what method you want to use and see where you are making any mistakes. So please post your work and you will receive help. Just to note, if you followed the guidelines you would have received some help by now. Thanks.
I suspect that you did not read our guidelines which state that you have to show us your work and state where you are stuck. In this way we know exactly what method you want to use and see where you are making any mistakes. So please post your work and you will receive help. Just to note, if you followed the guidelines you would have received some help by now. Thanks.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
These are both rather challenging, so clearly they were given to you as a challenge, and I should leave as much as possible for you to do.
For #49, I might start by using the fact that
That is, you can interchange the base and the argument of the log in the exponent. This lets you make x the base everywhere. There are several more tricks I see that can be used; your task is to discover at least one of them!
We'll also want to know what lg means in your context. I presume it is a log, but what base is assumed?
For #50, I would start by changing the bases of the logs so they are all the same. I haven't gone beyond that.
For #49, I might start by using the fact that
[MATH]a^{log_c b} = (c^{log_c a})^{log_c b} = c^{log_c a\cdot log_c b}= c^{log_c b\cdot log_c a} = (c^{log_c b})^{log_c a} = b^{log_c a}[/MATH].
That is, you can interchange the base and the argument of the log in the exponent. This lets you make x the base everywhere. There are several more tricks I see that can be used; your task is to discover at least one of them!
We'll also want to know what lg means in your context. I presume it is a log, but what base is assumed?
For #50, I would start by changing the bases of the logs so they are all the same. I haven't gone beyond that.
In 49, I have [MATH]x^{\log_{10}7}-x^{\log_{10}3}=\frac{40}{21}x^{\log_{10}\sqrt{3}} *x^{\log_{10}\sqrt{7}}[/MATH], and I have no idea what to do
D
Deleted member 4993
Guest
Now you can use:In 49, I have [MATH]x^{\log_{10}7}-x^{\log_{10}3}=\frac{40}{21}x^{\log_{10}\sqrt{3}} *x^{\log_{10}\sqrt{7}}[/MATH], and I have no idea what to do
\(\displaystyle \log_a(b)^c \ = \ \ c * \log_a(b)\)
To simplify further.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
Just do whatever you can do, one step at a time. It looked like a mess to me, too, until I persevered!
One thing you can do is to combine the two exponentials on the right. Another is to deal with those square roots.
If we replace the logs with parameters, the equation will now look like
Now try dividing by the exponential on the right ... then there will be some bigger tricks!
One thing you can do is to combine the two exponentials on the right. Another is to deal with those square roots.
If we replace the logs with parameters, the equation will now look like
[MATH]x^a - x^b = kx^{\frac{a+b}{2}}[/MATH]
Now try dividing by the exponential on the right ... then there will be some bigger tricks!
