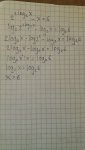hopefullynottaken
New member
- Joined
- Oct 4, 2017
- Messages
- 1
Can somebody tell me what am i doing wrong here?
\(\displaystyle 2^{2\log_2(x)}\, -\, x\, =\, 6\)
\(\displaystyle log_2\left(2^{2\log_2(x)}\right)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle 2\, \log_2(x)\, \cdot\, \log(2^2)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle 2\, \log_2(x)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle \log_2(x^2):x\, =\, \log_2(6)\)
\(\displaystyle \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle x\, =\, 6\)
\(\displaystyle 2^{2\log_2(x)}\, -\, x\, =\, 6\)
\(\displaystyle log_2\left(2^{2\log_2(x)}\right)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle 2\, \log_2(x)\, \cdot\, \log(2^2)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle 2\, \log_2(x)\, -\, \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle \log_2(x^2):x\, =\, \log_2(6)\)
\(\displaystyle \log_2(x)\, =\, \log_2(6)\)
\(\displaystyle x\, =\, 6\)
Attachments
Last edited by a moderator: