Local Extrema and Inflection Points

[SeekerOfDragons]

I'm once again, hoping to get confirmation on an answer I came up with on a problem.

Problem Reads:
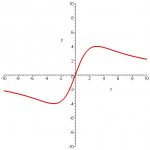
Sketch the graph and show all local extrema and inflection points of f(x) = 24x/(x^2 + 9)

I came up with:
Local Max at (3, 4)
Local Min at (-3, -4)
Inflection Points at ( sqrt(27), sqrt(12) ) and ( -sqrt(27), -sqrt(12) )

this results in
the graph decreasing (-infinity, -3), (3, infinity)
the graph increasing (-3, 3)

Concave up ( -sqrt(27), 0 )
Concave Down (0, sqrt (27) )

Hopefully I figured it correctly. If not, can you provide some direction on where my math went wrong?

 

[BigGlenntheHeavy]

Critical Points, (3,4),Max, (-3,-4),Min

Points of Inflection: (0,0),(3?3,2?3),(-3?3,-2?3)

See Graph.

[attachment=0:kr8puxtn]cap.jpg[/attachment:kr8puxtn]

 

[SeekerOfDragons]

so I was correct except for listing the inflection at (0,0) and reducing the square roots.

thanks for confirming my answers.

Hopefully you can help with my last question listed in the forum as well.