Hello, i have a test tomorrow and i need to know the answer to this asap.
Are these vectors linear dependent or independent:
1) {(1,1,3);(1,1,2)} What i have so far in this one:
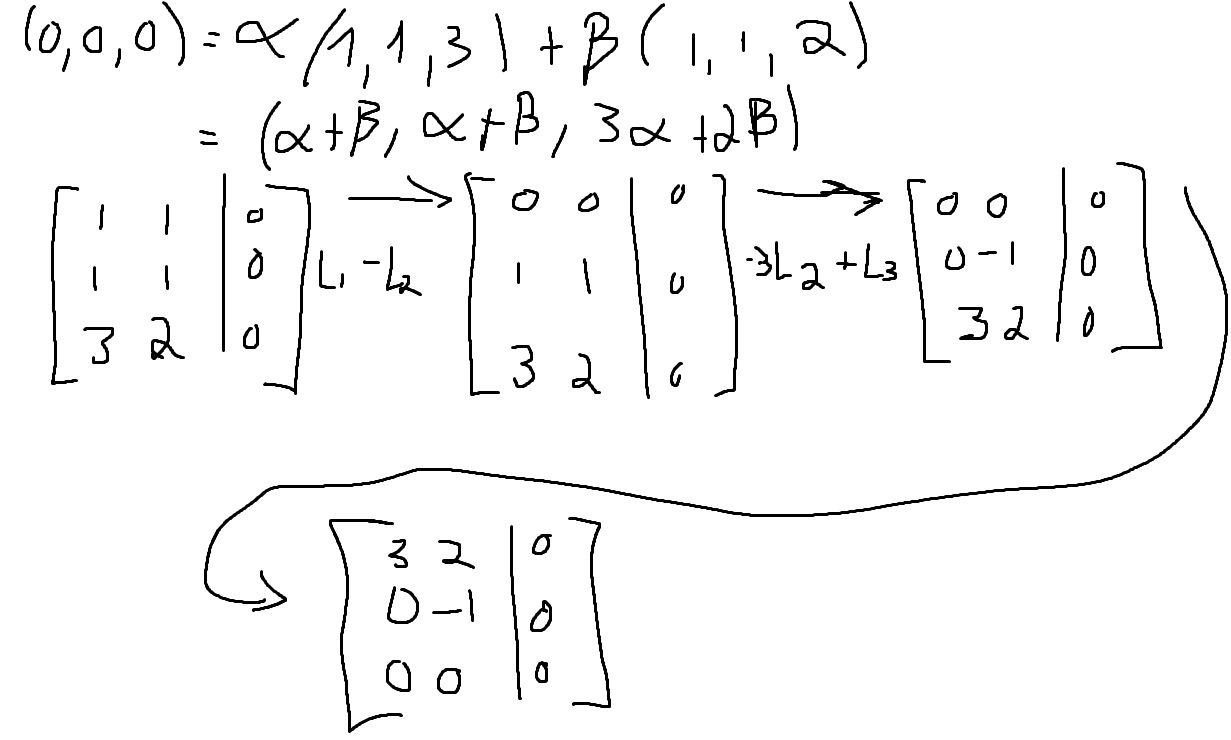
https://gyazo.com/c8b9157bcb74572efca5897536ba89be
2) {(1,1);(1,1);(3,2)}
thanks in advance.
Are these vectors linear dependent or independent:
1) {(1,1,3);(1,1,2)} What i have so far in this one:

https://gyazo.com/c8b9157bcb74572efca5897536ba89be
2) {(1,1);(1,1);(3,2)}
thanks in advance.
Last edited by a moderator:
