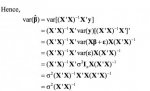In an assessment task on REML and manual matrix manipulation I need to write a mathematical proof. The question gives the final answer and a few rules I've attached as an image to make it easier to read. The following image is what I have taken from the lecture notes and is what I am supposed to use to obtain the proof.
\(\displaystyle \mbox{Prove that }\, var\left(\widehat{\beta}\right)\, =\, \left(X'\, \Sigma^{-1}\, X\right)^{-1}.\)
\(\displaystyle \mbox{If }\, \widehat{\beta}\, =\, \left(X'\, \hat{\Sigma}^{-1}\, X\right)^{-1}\, X'\, \hat{\Sigma}^{-1}\, y\, =\, Ay\, \mbox{ and }\, var\,(Ay)\, =\, A\, \Sigma\, A',\, \mbox{ where }\, var\,(y)\, =\, \Sigma\)
\(\displaystyle \mbox{Hence,}\)
. . . . .\(\displaystyle \begin{align} var\,(\hat{\beta})\, &=\, var\,\left[(X'\, X)^{-1}\, X'\, y\right]
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(y)\, \left[(X'\, X)^{-1}\, X' \right]'
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(X\beta\, +\, \epsilon)\, X\, (X'\, X)^{-1}
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(\epsilon)\, X\, (X'\, X)^{-1}
\\ \\ &=\, (X'\, X)^{-1}\, X'\, \sigma^2\, I_n \, X\, (X'\, X)^{-1}
\\ \\ &=\, \sigma^2\, (X'\, X)^{-1}\, X'\, X\, (X'\, X)^{-1}
\\ \\ &=\, \sigma^2\, (X'\, X)^{-1} \end{align}\)
Im assuming my biggest problem is likely a limited understanding of how the operations work when I'm trying to substitute E into the equations where var and sigma sqrd are featured.
Any help would be greatly appreciated.
\(\displaystyle \mbox{Prove that }\, var\left(\widehat{\beta}\right)\, =\, \left(X'\, \Sigma^{-1}\, X\right)^{-1}.\)
\(\displaystyle \mbox{If }\, \widehat{\beta}\, =\, \left(X'\, \hat{\Sigma}^{-1}\, X\right)^{-1}\, X'\, \hat{\Sigma}^{-1}\, y\, =\, Ay\, \mbox{ and }\, var\,(Ay)\, =\, A\, \Sigma\, A',\, \mbox{ where }\, var\,(y)\, =\, \Sigma\)
\(\displaystyle \mbox{Hence,}\)
. . . . .\(\displaystyle \begin{align} var\,(\hat{\beta})\, &=\, var\,\left[(X'\, X)^{-1}\, X'\, y\right]
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(y)\, \left[(X'\, X)^{-1}\, X' \right]'
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(X\beta\, +\, \epsilon)\, X\, (X'\, X)^{-1}
\\ \\ &=\, (X'\, X)^{-1}\, X'\, var\,(\epsilon)\, X\, (X'\, X)^{-1}
\\ \\ &=\, (X'\, X)^{-1}\, X'\, \sigma^2\, I_n \, X\, (X'\, X)^{-1}
\\ \\ &=\, \sigma^2\, (X'\, X)^{-1}\, X'\, X\, (X'\, X)^{-1}
\\ \\ &=\, \sigma^2\, (X'\, X)^{-1} \end{align}\)
Im assuming my biggest problem is likely a limited understanding of how the operations work when I'm trying to substitute E into the equations where var and sigma sqrd are featured.
Any help would be greatly appreciated.
Attachments
Last edited by a moderator: