Limits

[vsverduk]

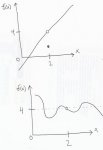
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2? Explain your reasoning.
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain your reasoning.
Post your solution on the Discussion Board titled Limit Reasoning.


This is the answer that I came up with. Am I missing something or is this correct?
For the first one you can conclude that all numbers for f(x) will not equal 4 but will lead up to 4 when they reach 2. In the second one if the answer is 4 as it approaches 2 then (x) cannot equal 2.

 

[mmm4444bot]

The value of a limit as x approaches 2 has nothing to do with the value of the function at x = 2.

So, if we're told that a limit is 4 when x approaches 2, we have no idea what the function is doing at x = 2. We only know that the function approaches 4 on either side of x = 2.

In fact, the function might not even be defined at x = 2, but the limit there can still exist.

If we're told that the function's value at x = 2 is 4, then we cannot say anything at all about the limit as x approaches 2 without knowing more about the function. (For example, if we're told that the function is linear, and it's value is 4 at x = 2, then we can say that the limit is 4 also. Without knowing that the function is smooth and continuous -- like a linear function -- we cannot know about the limit.)

I'm not sure what you're thinking by saying that no other values of the function can be 4 if the function has a value of 4 at x = 2 because that is not true.

I will draw some sloppy pictures and post there here in a few minutes …

 

[mmm4444bot]

Double-click images to expand.

Here's a couple examples where the function f(2) = 4, but no limit exists at x = 2.

[attachment=1:2p2xkdkr]lim1.JPG[/attachment:2p2xkdkr]

Here's a couple examples where the limit at x = 2 is 4, but f(2) does not equal 4 in the top example and f(2) is not even defined in the bottom example.

Also, in the bottom example, we can see that f takes on the value 4 at many places over its domain.

[attachment=0:2p2xkdkr]lim2.JPG[/attachment:2p2xkdkr]