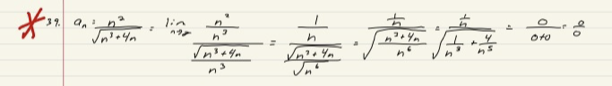This approach isn't specific to sequences, but that's where it came up in the textbook. The following example divides both the numerator and the denominator by n, the highest power of n in the denominator (this technique is explained in the "Solution" section).

So both are divided by n. No problem. That makes sense to me. But in the following example, the solution divides both the numerator and denominator by [imath]n^2[/imath]. But isn't the highest power of n in the denominator [imath]\sqrt{n}[/imath] instead of [imath]n^2[/imath]? The "Solution" for example 4 shown above says divide by the highest power of n that occurs in the denominator. This seems to depart from that.

So why is it [imath]n^2[/imath] in Example 5?

So both are divided by n. No problem. That makes sense to me. But in the following example, the solution divides both the numerator and denominator by [imath]n^2[/imath]. But isn't the highest power of n in the denominator [imath]\sqrt{n}[/imath] instead of [imath]n^2[/imath]? The "Solution" for example 4 shown above says divide by the highest power of n that occurs in the denominator. This seems to depart from that.

So why is it [imath]n^2[/imath] in Example 5?