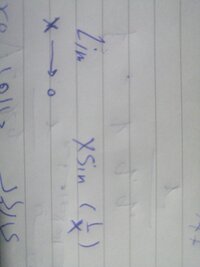Limit.. Zero or one?

[Nwr]

Calcouls book solved it zero but i solve it one.. Where is the wrong step that i did?

 

[pka]

Calcouls book solved it zero but i solve it one.. Where is the wrong step that i did?

Please post a complete readable of a statement of the problem as well as your work.
Do not post an unreadable image. Thank you.

 

[Steven G]

Sin(x) (or even sin(1/x)) is ALWAYS between -1 and 1. Well, sin(1/x) is undefined but that doesn't matter as x approaches 0 so it will never be 0

Consider the last inequality (assume x is not 0) -1< sin(1/x) < 1. Multiplying by x>0 we get -x< xsin(1/x) < x. What does the squeeze theorem tell you when x approaches 0⁺.

Now you consider what happens when x<0.

 

[Harry_the_cat]

We can't help you if we can't read it!!

 

[Steven G]

If x was going to infinity, then the answer would be 1.

Yes, lim x->0 (sinx/x) =1. Note that the angle x and the denominator are the same AND as x->0 the angle and the denominator also go to 0.

For example: lim as x->5 sin(x-5)/(x-5) = 1 since the angle and the denominator are the same and as x->5, (x-5)->0

In your problem lim x->0 sin(1/x)/(1/x) you do have the angle and the denominator being the same BUT as x->0, 1/x is NOT going to 0--it's going to infinity!!!!


You also replaced sin(1/x)/(1/x) with 1 in your work which is not true. Even sinx/x is not 1. Remember that a fraction is 1 when the numerator and denominator are the same! sinx is always between -1 and 1 while x can be any value. Consider sin(7)/7. This can't be 1 since sin(7) and 7 are not equal!! It is the lim x->0 sinx/x which equals 1.

 

[Harry_the_cat]

Forget about your limit rules and think about what is going on.

\(\displaystyle -1\leq sin (\theta)\leq 1\) for all values of \(\displaystyle \theta\).

So, \(\displaystyle -1\leq sin (1/x)\leq 1\).

Now look at \(\displaystyle x\times \sin(\frac{1}{x})\).

If \(\displaystyle x\to 0\) then you have a value getting closer and closer to 0 multiplied by a value that lies between -1 and 1.

eg

\(\displaystyle 0.00001 \times \)(a number between -1 and 1).

\(\displaystyle 0.00000000001\times \)(a number between -1 and 1), etc.

Surely this is approaching 0.

 

[Steven G]

Forget about your limit rules and think about what is going on.

\(\displaystyle -1\leq sin (\theta)\leq 1\) for all values of \(\displaystyle \theta\).

So, \(\displaystyle -1\leq sin (1/x)\leq 1\).

Now look at \(\displaystyle x\times \sin(\frac{1}{x})\).

If \(\displaystyle x\to 0\) then you have a value getting closer and closer to 0 multiplied by a value that lies between -1 and 1.

eg

\(\displaystyle 0.00001 \times \)(a number between -1 and 1).

\(\displaystyle 0.00000000001\times \)(a number between -1 and 1), etc.

Surely this is approaching 0.

I posted that information 1st!!

 

[Harry_the_cat]

I posted that information 1st!!

Yeah yeah!! Just wait while I look for my gold stars.