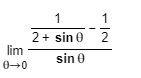Limit, theta approaches 0

[Bigglesworth95]

Hello all,

I am working on my Calculus I hw, and these problems and ones like them have stumped me. I know that you're supposed to only submit one problem per forum post, but I figured I would put two up and if you would like to help me with either or both of them than you can please do so.

In case you don't wish to open the attached files, I have written out the problems below. My apologies for the messy appearance of typed out math problems. Anyways:

1) lim_Theta-->0 [ 1/(2+sin theta) - 1/2 ]/sin theta

2) lim_x-->0 5(cosx -1)/sin²x

As an addendum, here is what I did for problem

1: I gave the fractions in the numerator a shared base of 2(2+sin theta). This worked out to 2 - (2+sin theta)/2(2+sin theta), which of course simplifies to sin theta/2(2+sin theta) when you distribute the negative one in the numerator here.

2: I then brought the denominator sin theta up to the numerator to give me sin2 theta/2(2+sin theta)

3. From here there was no more simplifying to be done, so I plugged in 0 and arrived at 0 for a limit, which is incorrect.

Thank you so much for the help!

If you wish to answer, please list out your steps and explain what you're doing if you wouldn't mind. I am having a really tough time figuring out how to get to the bottom of these questions and wish to get over this hump as quickly and thoroughly as possible.

Thanks again!!!!

 

[MarkFL]

I would simplify the first limit to read:

[MATH]L=-\lim_{\theta\to0}\frac{\sin(\theta)}{2\sin(\theta)(2+\sin\theta)}=-\lim_{\theta\to0}\frac{1}{2(2+\sin\theta)}[/MATH]
Now you can use direct substitution to determine the limit. What do you get?

 

[MarkFL]

For the second limit, I would write:

[MATH]\frac{5(\cos(x)-1)}{\sin^2(x)}=-\frac{5(1-\cos(x))}{(1+\cos(x))(1-\cos(x))}=-\frac{5}{1+\cos(x)}[/MATH]
Can you proceed?

 

[Bigglesworth95]

Thank you very much for your help! I just finished the first problem, and got 1/4. I am working on the second one now but I am sure it will go well. Thanks for reminding me about that identity regarding sin^2.

 

[Steven G]

What is going wrong with the 2nd problem. Just substitute x=0 in the expression which MarkFL gave you.