I am trying to figure out how to prove the equality I circled below in red. I have figured out how to prove the text in blue but don't know how to use that to prove the equality I circled in red.
Below I will post the givens I'm trying to use and my guess of how to prove it.
P.S. I understand this only proves the chain rule in the special case where \(\displaystyle \Delta u \neq 0 \). This is from Stewart's Calculus and he does mention that this is not a full proof but I'm very curious how to prove this special case anyway.

I'm not sure if I'm using the right givens below.
In their blue form it looks like I will be able to use the transitive property of implication \(\displaystyle (a \rightarrow b \wedge b \rightarrow c) \rightarrow (a \rightarrow c)\) if I can always let the \(\displaystyle \epsilon\) from the 1st given equal the \(\displaystyle \delta\) from the second line.
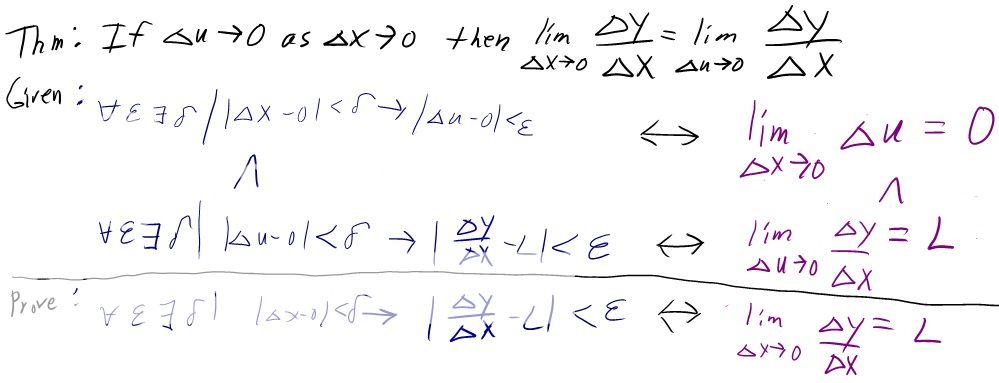
Below I will post the givens I'm trying to use and my guess of how to prove it.
P.S. I understand this only proves the chain rule in the special case where \(\displaystyle \Delta u \neq 0 \). This is from Stewart's Calculus and he does mention that this is not a full proof but I'm very curious how to prove this special case anyway.

I'm not sure if I'm using the right givens below.
In their blue form it looks like I will be able to use the transitive property of implication \(\displaystyle (a \rightarrow b \wedge b \rightarrow c) \rightarrow (a \rightarrow c)\) if I can always let the \(\displaystyle \epsilon\) from the 1st given equal the \(\displaystyle \delta\) from the second line.
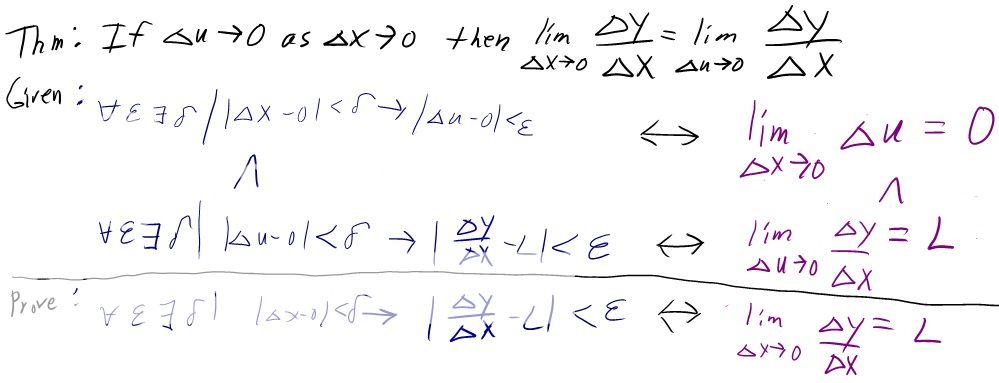
Last edited:

