Limit of Function

[turophile]

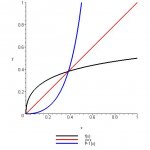
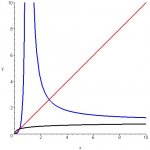
Here's the problem statement: Find lim f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](x) as x approaches 2 for f(x) = 1 / [ 1 + 1 / sqrt(x) ].

First, I found f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](x):

1 / [ 1 + 1 / sqrt(x) ] = y

1 + 1 / sqrt(x) = 1 / y

1 / sqrt(x) = 1 / y - 1 = (1 - y) / y

sqrt(x) = y / (1 - y)

x = y[sup:iw3d6lgg]2[/sup:iw3d6lgg] / (1 - y)[sup:iw3d6lgg]2[/sup:iw3d6lgg]

So, f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](x) = x[sup:iw3d6lgg]2[/sup:iw3d6lgg] / (1 - x)[sup:iw3d6lgg]2[/sup:iw3d6lgg], and f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](2) = 2[sup:iw3d6lgg]2[/sup:iw3d6lgg] / (1 - 2)[sup:iw3d6lgg]2[/sup:iw3d6lgg] = 4 / (-1)[sup:iw3d6lgg]2[/sup:iw3d6lgg] = 4, so lim f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](x) as x approaches 2 = 4.

However, the answer in my textbook says lim f [sup:iw3d6lgg]- 1[/sup:iw3d6lgg](x) as x approaches 2 for f(x) = 1 / [ 1 + 1 / sqrt(x) ] is not defined.

My question: Am I wrong, or is my textbook?

 

[BigGlenntheHeavy]

$\displaystyle \lim_{x\to1}[f^{-1}(x)] \ is \ undefined, \ did \ you \ post \ correctly?$

 

[turophile]

I double checked the wording of the exercise, and it is indeed the limit of f(x) as x approaches 2, not as x approaches 1.

 

[BigGlenntheHeavy]

$\displaystyle f[f^{-1}(x)] \ = \ x \ = \ f^{-1}[f(x)]$

$\displaystyle f(x) \ = \ \frac{\sqrt x}{\sqrt x+1}, \ x \ \ne 0 \ and \ f^{-1}(x) \ = \ \frac{x^2}{(1-x)^2}, \ 0 \ < \ x < \ 1, \ is \ true.$

$\displaystyle The \ domain \ of \ f^{-1}(x) \ is \ (0,1), \ hence \ 2 \ is \ undefined.$

$\displaystyle Note: \ f^{-1}(2/3) \ = \ 4 \ and \ f(4) \ = \ 2/3, \ but \ f^{-1}(3/2) \ =9 \ and \ f(9) \ = \ 3/4, \ not \ 3/2.$

$\displaystyle Obviously, \ when \ we \ found \ f^{-1}(x), \ we \ pick \ up \ some \ extraenous \ roots.$

$\displaystyle See \ graph \ below.$

[attachment=1:2kirqyce]ggg.jpg[/attachment:2kirqyce]

$\displaystyle Here \ is \ the \ same \ graph \ as \ above \ expanded.$

[attachment=0:2kirqyce]hhh.jpg[/attachment:2kirqyce]