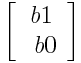lim (cos(2) - cos(x))
x->infinity
Sorry don't know how to put the infinity sign in there. My question is that the text I am reviewing says that this limit does not exist and I don't understand why. I know the following about limits not existing:
A limit does not exist if:
1. The function is oscillating at/around the point the limit is being taken at
2. The function approaches a different number from the left(neg) than from the right(pos) side.
3. in general, a limit does not exist if evaluating the limit, it does not settle down on a single number.
Thanks for any help on this. I'm sure it's really easy and I'm just missing some basic thing!!
x->infinity
Sorry don't know how to put the infinity sign in there. My question is that the text I am reviewing says that this limit does not exist and I don't understand why. I know the following about limits not existing:
A limit does not exist if:
1. The function is oscillating at/around the point the limit is being taken at
2. The function approaches a different number from the left(neg) than from the right(pos) side.
3. in general, a limit does not exist if evaluating the limit, it does not settle down on a single number.
Thanks for any help on this. I'm sure it's really easy and I'm just missing some basic thing!!