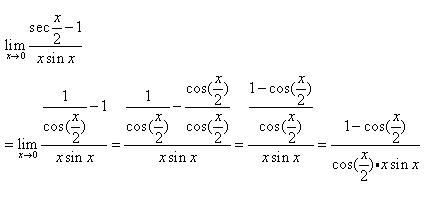
lim x->0 [sec(x/2)-1]/[xsin(x)]
- Thread starter tdotgirl
- Start date
I don't like to use L'Hopital unless I have to. I think I'll use it on this one. Perhaps pka, Soroban, Skeeter, or someone will be along with a non-L'Hopital method. It's even quite precarious with L'Hopital.
Assuming you're allowed to use it.
\(\displaystyle \L\\\lim_{x\to\0}\frac{sec(\frac{x}{2})-1}{xsin(x)}\)
Differentiate num. and den. and we get:
\(\displaystyle \L\\\lim_{x\to\0}\frac{\frac{1}{2}sec(\frac{x}{2})tan(\frac{x}{2})}{xcos(x)+sin(x)}\)
W're still in indeterminate form, so do it again....WHEW:
\(\displaystyle \L\\\lim_{x\to\0}\frac{\frac{1}{2}\left[sec(\frac{x}{2})(\frac{3}{2}sec^{2}(\frac{x}{2})-1)\right]}{2cos(x)-xsin(x)}\)
This looks horrendous, but if you look you can see. sec(0)=1 and cos(0)=1
So, we have:
\(\displaystyle \L\\\frac{\frac{1}{2}(\frac{1}{2})}{2}=\frac{1}{8}\)
The trick is to get rid of that infernal xsin(x) in the denominator because of dividing by 0. This may be hackneyed, but it works.
Assuming you're allowed to use it.
\(\displaystyle \L\\\lim_{x\to\0}\frac{sec(\frac{x}{2})-1}{xsin(x)}\)
Differentiate num. and den. and we get:
\(\displaystyle \L\\\lim_{x\to\0}\frac{\frac{1}{2}sec(\frac{x}{2})tan(\frac{x}{2})}{xcos(x)+sin(x)}\)
W're still in indeterminate form, so do it again....WHEW:
\(\displaystyle \L\\\lim_{x\to\0}\frac{\frac{1}{2}\left[sec(\frac{x}{2})(\frac{3}{2}sec^{2}(\frac{x}{2})-1)\right]}{2cos(x)-xsin(x)}\)
This looks horrendous, but if you look you can see. sec(0)=1 and cos(0)=1
So, we have:
\(\displaystyle \L\\\frac{\frac{1}{2}(\frac{1}{2})}{2}=\frac{1}{8}\)
The trick is to get rid of that infernal xsin(x) in the denominator because of dividing by 0. This may be hackneyed, but it works.
