l'hospital's rule

[rae27]

I need help with lim as x-->0+ x^(2/x). I know the answer is 0, but I don't understand why. Could someone explain it? Thanks.

 

[galactus]

This may be considered sloppy by some, but this is one way to look at it. \(\displaystyle 0^{\infty}\) is not considered an indeterminate form, as opposed to \(\displaystyle {\infty}^{0}\), which is indeterminate.

Because \(\displaystyle \lim_{x\to \infty}0^{x}=0\)

\(\displaystyle \lim_{x\to 0^{+}}x^{\frac{2}{x}}\)

\(\displaystyle =\displaystyle\left(\lim_{x\to 0^{+}} x\right)^\Large{{\left(2 \lim_{x\to 0^{+}}\frac{1}{x}\right)}\)

\(\displaystyle =\left(\lim_{x\to 0^{+}} x\right)^{\infty}=0^{\infty}=0\)

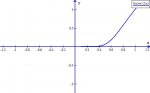
Here's the graph. See why it heads toward 0 if we approach 0 from the right?.

 

[PAULK]

I need help with lim as x-->0+ x^(2/x). I know the answer is 0, but I don't understand why. Could someone explain it? Thanks.

I think you handle it like this. Any time you have some complicated exponential, try logs:

Let y = x^(2/x)

ln y = (2/x) ln x

Now try letting x -> 0.

2/x --> +infinity.
ln x --> - infinity.

ln y = (2/x) ln x -> - infinity.

So y -> e^(-infinity) = 0

 

[rae27]

Thanks. I can see it now.