L'Hospita?: find a, b, so lim (sin(2x)/x^3 + a + b/x^2) = 0

[scrum]

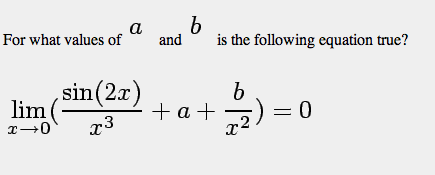
I've tried plugging in random values for a in a computer graphing program, and it moves the graph up and down but doesn't move a value to zero. I've tried chainging the values of b as well but they just change the curvature of it and don't move a value onto the zero.

I'm sorta lost on this one but i think it has something to do with L'hospital as thats what we're learning.

 

[Unco]

Re: L'Hospital I think

Combine the terms into a single quotient and apply L'Hopital's rule as many times as necessary. The sufficient condition that both numerator and denominator are zero in order to apply the rule gives b at some stage and from the final form you can get a.

 

[scrum]

Re: L'Hospital I think

I'm still sorta confused. what do you mean by combine the terms into a single quotient?

 

[o_O]

Re: L'Hospital I think

\(\displaystyle \frac{sin(2x)}{x^{3}} + a + \frac{b}{x^{2}}\)

\(\displaystyle =\frac{sin(2x)}{x^{3}} + a \cdot \frac{x^{3}}{x^{3}} + \frac{b}{x^{2}} \cdot \frac{x}{x}\)

\(\displaystyle =\frac{sin(2x)}{x^{3}} + \frac{ax^{3}}{x^{3}} + \frac{bx}{x^{3}}\)

\(\displaystyle =\frac{sin(2x) + ax^{3} + bx}{x^{3}}\)

Now apply l'hopital's rule as many times as you want and you'll eventually be able to solve for a (and b along the way). Just keep in mind that you can only apply it when you have an indeterminate form (0/0 in this case). So you want the numerator to equal to 0 all the way through even when the denominator disappears (keeping in mind applying l'hopital's rule will always result in the limit being 0).