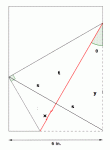
Length of crease of folded paper
- Thread starter crazylum
- Start date
Thanks galactus but the answer is \(\displaystyle L=\frac{3}{\sin\theta\cos^2\theta}\). I see where you're going and I'll see what I come up with. If it's any help the problem is presented in the chapter of the book that deals with half angle, double angle and sum to product formulas, so I know they come into play. Just can't figure out which one to use.
Draw another 6" horizontal line from the end of red line L.
Thr right triangle that this will create is similar to the smaller right triangle at bottom left.
By the way, are you sure your diagram is correct?
Seems to me the end of red line L should end up at the corner of the rectangle,
else there's no possible way to calculate that side of the rectangle.
Thr right triangle that this will create is similar to the smaller right triangle at bottom left.
By the way, are you sure your diagram is correct?
Seems to me the end of red line L should end up at the corner of the rectangle,
else there's no possible way to calculate that side of the rectangle.
Draw a new line from the folded corner (middle left) to its original position (lower right). This new line and line L are the diagonals of a kite. (The two original large triangles form a kite.) They are, therefore, perpendicular to each other.
Adding the new line creates many similar triangles within the figure.
Note also that the new line’s length is (cos theta)/6. When split in two, the two segments are both altitudes of the large triangles and legs of smaller, similar triangles.
Hope that helps.
Adding the new line creates many similar triangles within the figure.
Note also that the new line’s length is (cos theta)/6. When split in two, the two segments are both altitudes of the large triangles and legs of smaller, similar triangles.
Hope that helps.
D
Deleted member 4993
Guest
I believe there is something missing in the problem statement.
Without changing L or @ - we can increase the side of the original rectangle to 8" (from 6") - or some other length. How does "3" come into the picture?
Without changing L or @ - we can increase the side of the original rectangle to 8" (from 6") - or some other length. How does "3" come into the picture?
I will be da***ed, I just got it!!! 
I went off wjm's idea of drawing the line from corner to corner and creating the perpendicular to the crease. That makes the kite looking figure.
As he stated, that makes this line have length \(\displaystyle \frac{6}{cos{\theta}}\). Half of this length we'll call s and it has length \(\displaystyle s=\frac{3}{cos{\theta}}\)
Let's denote L=x+t. From the diagram and s, \(\displaystyle x=\frac{3tan{\theta}}{cos{\theta}}\)
And \(\displaystyle t=\frac{3}{cos{\theta}tan{\theta}}\)
Since L=x+t, add them: \(\displaystyle \frac{3tan{\theta}}{cos{\theta}}+\frac{3}{cos{\theta}tan{\theta}}=\boxed{\frac{3}{sin{\theta}cos^{2}{\theta}}}\)
I went off wjm's idea of drawing the line from corner to corner and creating the perpendicular to the crease. That makes the kite looking figure.
As he stated, that makes this line have length \(\displaystyle \frac{6}{cos{\theta}}\). Half of this length we'll call s and it has length \(\displaystyle s=\frac{3}{cos{\theta}}\)
Let's denote L=x+t. From the diagram and s, \(\displaystyle x=\frac{3tan{\theta}}{cos{\theta}}\)
And \(\displaystyle t=\frac{3}{cos{\theta}tan{\theta}}\)
Since L=x+t, add them: \(\displaystyle \frac{3tan{\theta}}{cos{\theta}}+\frac{3}{cos{\theta}tan{\theta}}=\boxed{\frac{3}{sin{\theta}cos^{2}{\theta}}}\)
Attachments
D
Deleted member 4993
Guest
Why would that new line (joining the corner to the right-angled-triangle) be perpendicular to "L" and be bisected by "L"? I think it will be true only when the "original two big triangles" are equal?
My original "problem" - extend the base (of the rectangle) to say 8" and redraw the lines without changing "L" or "@"?
how does the answer to the problem change?
If you move the point - of intersection (intersection of "L" to the base) to "near the corner" - so that the "little triangle"(original) will be very little - and the two larger triangles will be different shapes - then you'll see that the new line is not perpendicular to "L".
My original "problem" - extend the base (of the rectangle) to say 8" and redraw the lines without changing "L" or "@"?
how does the answer to the problem change?
If you move the point - of intersection (intersection of "L" to the base) to "near the corner" - so that the "little triangle"(original) will be very little - and the two larger triangles will be different shapes - then you'll see that the new line is not perpendicular to "L".
Thanks Subhotosh Khan, wjm and especially galactus. I think you nailed it galactus. Subhotosh is right, I didn't include all of the text to the problem. The original problem stated that the lower right corner of the paper was folded to meet some point on the left hand side and that the length of L was determined by \(\displaystyle \theta\). There are, of course, a finite number of points that the corner could meet on the opposite side, but the diagram I used I created with Geogebra following the illustration in the text. I'm going to work this problem from galactus' point of view and see what happens. I think there may be another way to approach this using double-angle, half-angle or sum to product trigonometry formulas. I'll let you know. I really do appreciate everyone's input on this. This is the best forum ever.