Let

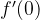 , we need to compute the left-hand limit and the right-hand limit
, we need to compute the left-hand limit and the right-hand limit
I've solved similar problems, but I can't seem to get the left hand limit. Using lim x-->0+ (f(x)-f(a))/(x-a), I got the right hand limit to equal 4x, which is correct according to the program I'm using, but using the same formula for limx-->0-((-4x^2+7x)-0)/(x-0) equals -4x+7, which apparently is incorrect. I'm just not sure what I'm doing wrong.

According to the definition of derivative, to compute 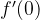
I've solved similar problems, but I can't seem to get the left hand limit. Using lim x-->0+ (f(x)-f(a))/(x-a), I got the right hand limit to equal 4x, which is correct according to the program I'm using, but using the same formula for limx-->0-((-4x^2+7x)-0)/(x-0) equals -4x+7, which apparently is incorrect. I'm just not sure what I'm doing wrong.
