You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I've watched too many videos but I couldn't figure out how to solve it. Can someone help me??
- Thread starter Raehya
- Start date
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,104
What do you have difficulty with?
Have you seen the Khan Academy page on the subject :
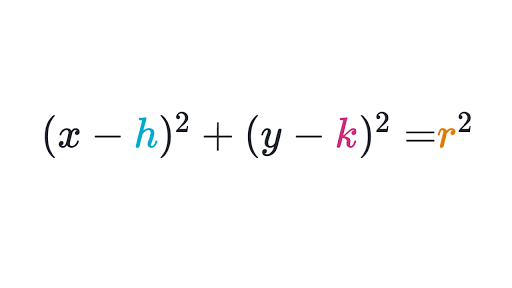
 www.khanacademy.org
www.khanacademy.org
Have you seen the Khan Academy page on the subject :
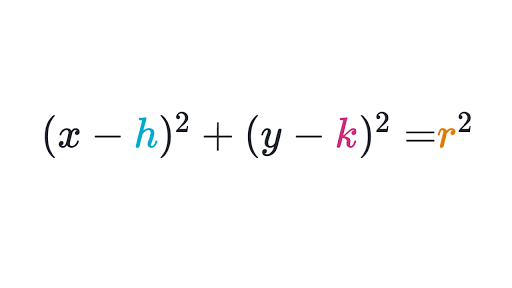
Circle equation review | Analytic geometry (article) | Khan Academy
Review the standard and expanded forms of circle equations, and solve problems concerning them.
D
Deleted member 4993
Guest
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 544
Beer induced ramblings follow.
Solved. Thank you for that thought-provoking, intellectually invigorating mental exercise. Next problem please.
The Highlander
Senior Member
- Joined
- Feb 18, 2022
- Messages
- 1,059
@Raehya
Completing the square is a perfectly valid approach, when a circle's equation is given in the "Expanded Form"
At least that is the way it is taught here in Scotland (and, I believe, throughout the rest of the UK too; other countries may differ in their approaches, of course).
Please watch this video.
(It won't hurt to watch just one more video, especially if it directly addresses your problem!)
This is another 'lesson' prepared with Scottish Higher Maths students in mind (by another Scottish Maths teacher) and the very first screen explains everything you need to know but, if you persevere and watch all the way through the examples provided, the third example shows you exactly how to solve your particular problem.
Hope that helps.
PS: If you decide to jump in without watching the examples, please be sure to follow @Steven G's advice:-
Completing the square is a perfectly valid approach, when a circle's equation is given in the "Expanded Form"
\(\displaystyle x^2+y^2+2gx+2fy+c=0\).
The centre's coordinates can be read (almost) directly from the equation, and we can calculate the radius using a simple formula: \(\displaystyle \left(\sqrt{g^2+f^2–c}\right)\).
At least that is the way it is taught here in Scotland (and, I believe, throughout the rest of the UK too; other countries may differ in their approaches, of course).
Please watch this video.
(It won't hurt to watch just one more video, especially if it directly addresses your problem!)
This is another 'lesson' prepared with Scottish Higher Maths students in mind (by another Scottish Maths teacher) and the very first screen explains everything you need to know but, if you persevere and watch all the way through the examples provided, the third example shows you exactly how to solve your particular problem.
Hope that helps.
PS: If you decide to jump in without watching the examples, please be sure to follow @Steven G's advice:-
because, as the video's first screen explains, the \(\displaystyle x^2\) & \(\displaystyle y^2\) coefficients must both be 1 (for the method to "work"!) However, I strongly advise you to watch at least the first three examples provided in the video and, at the very least, study the third example if no others.1st divide all terms by 4.
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
I've watched too many videos but I couldn't figure out how to solve it.
Can someone help me??
Hello Raehya. What kind of help do you need? Do you have any specific questions about what you've seen in prior videos or how their explanations apply to your exercise?
Also, please take time to read our posting guidelines. In case you didn't save the link you were provided, a summary link appears below. Thank you!
Posting Guidelines (Summary)
Welcome to our tutoring boards! :) This page summarizes main points from our posting guidelines. As our name implies, we provide math help (primarily to students with homework). We do not generally post immediate answers or step-by-step solutions. We don't do your homework. We prefer to help...
www.freemathhelp.com
The Highlander
Senior Member
- Joined
- Feb 18, 2022
- Messages
- 1,059
You are absolutely right! I should, indeed, have typed: \(\displaystyle \left(\sqrt{g^2+f^2\textcolor{red}{-c}}\right)\); my bad! ?I believe there's an error in your formula. It should be minus [imath]c[/imath].
The video that I have directed the OP to does not, of course, have the same error in it and makes it clear that the correct formula for the radius is: \(\displaystyle \left(\sqrt{g^2+f^2-c}\right)\)
However, watching the video myself, I note that the speaker does make a slight boob almost at the end of the first slide when he says: "So, \(\displaystyle g^2+f^2-c\) must equal zero in order for it to be a circle" when he clearly meant to say: "... must be greater than zero in order for it to be a circle"! ?
I guess we all make (small?) mistakes occasionally but thanks for pointing that out @BigBeachBanana. ??

