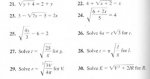Hello, jayson!
That's just great! .You can't do the first problem.
This means you've never heard of Radical Equations ... ever!
So why were you assigned two dozen such problems?
Okay, here is your missing lesson.
Isolate the radical..(Get the square root "alone" on one side of the equation.)
Square both sides of the equation ... carefully!
Solve the resulting equation.
Check all answers ... some may be extraneous.
\(\displaystyle (23)\;\;3 - \sqrt{7x-3} \:=\:2x\)
\(\displaystyle \text{We have: }\qquad\;\;\; 3 - 2x \;=\;\sqrt{7x-3}\)
\(\displaystyle \text{Square: }\qquad\;\;(3-2x)^2 \;=\;\left(\sqrt{7x-3}\right)^2\)
. . . . . . . .\(\displaystyle 9 - 12x + 4x^2 \;=\;7x-3\)
. . . . . . .\(\displaystyle 4x^2 - 19x + 12 \;=\;0\)
\(\displaystyle \text{Factor: }\;(4x-3)(x-4) \;=\;0\)
\(\displaystyle \text{Hence: }\:\begin{Bmatrix}4x-3 \:=\:0 & \Rightarrow & x \:=\:\frac{3}{4} \\ x-4\:=\:0 & \Rightarrow & x \:=\:4 \end{Bmatrix}\)
Check. \(\displaystyle x = \frac{3}{4}\)
\(\displaystyle \text{Does }\,3 - \sqrt{7(\frac{3}{4})-3} \;=\;2(\frac{3}{4})\:?\)
. . \(\displaystyle 3 - \sqrt{\frac{21}{4} - 3} \;=\; 3 - \sqrt{\frac{9}{4}} \;=\;3 - \frac{3}{2} \;=\;\frac{3}{2}\) .Yes!
Hence, \(\displaystyle x = \frac{3}{4}\) is a solution.
Check..\(\displaystyle x = 4\)
\(\displaystyle \text{Does }\,3 - \sqrt{7(4) - 3} \;=\;2(4)\,?\)
. . \(\displaystyle 3 - \sqrt{25} \;=\;3-5 \;=\;-2\) .No!
Hence, \(\displaystyle x = 4\) is an extraneous solution.
Therefore, the only solution is. \(\displaystyle x = \frac{3}{4}\)