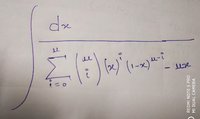Is this Integration has a solution

[anita chandra]

I was trying to solve a differential equation that I defined to study the dynamics of a system. Meanwhile, I encounter integration. The integration is shown in the image below. I tried some solutions but I am failed to get a solution. In one solution, I took "x" common from the denominator terms and then apply a partial method to solve the equation. But that does not work. I request the members of this forum to give me at least an intuition to how can I solve this integration. Thanks a lot.

 

[LCKurtz]

Isn't that sum in the denominator just [MATH](x + (1-x))^n[/MATH]?

 

[anita chandra]

Isn't that sum in the denominator just [MATH](x + (1-x))^n[/MATH]?

yes, the first part of the denominator is a binomial form. so my integral part is 1/ (x+(1-x))^n + mu*x where mu is a constant.

Is the first part can be simply be replaced by 1. Do we can simply write replace those term by 1? As the sum of the binomial term is 1.

 

[anita chandra]

yes, the first part of the denominator is a binomial form. so my integral part is 1/ (x+(1-x))^n + mu*x where mu is a constant.

Is the first part can be simply be replaced by 1. Do we can simply write replace those term by 1? As the sum of the binomial term is 1.

If I will replace the whole term with 1 then I can easily solve the integral. My question is does we can simply this equation like this.

Thanks for ur reply LCKurtz

 

[LCKurtz]

Yes. The quantity is [MATH]1[/MATH] so put that in and proceed.

 

[anita chandra]

Yes. The quantity is [MATH]1[/MATH] so put that in and proceed.

Thanks a lot for proper suggestion.