Is Pi(π) repeating itself?
- Thread starter SirBuy
- Start date
D
Deleted member 4993
Guest
Please read:
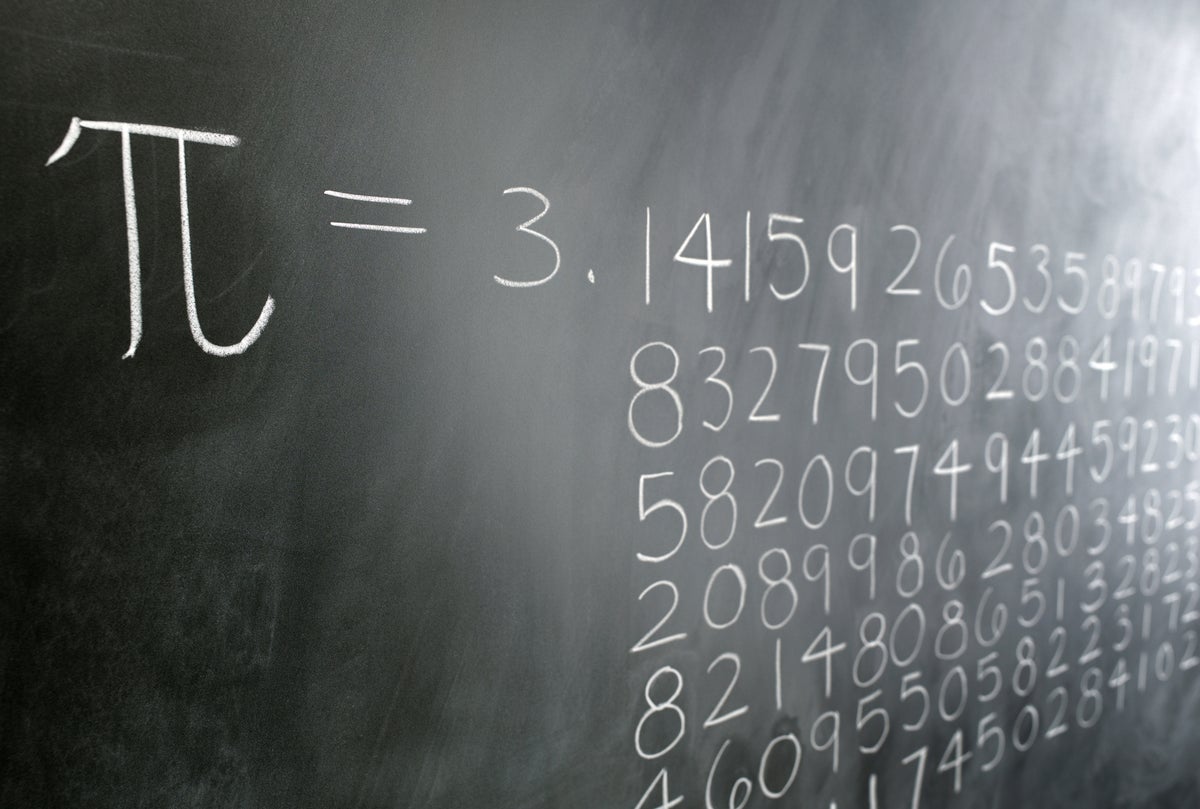
www.scientificamerican.com
If still have question/s, please come back and ask.
What Is Pi, and How Did It Originate?
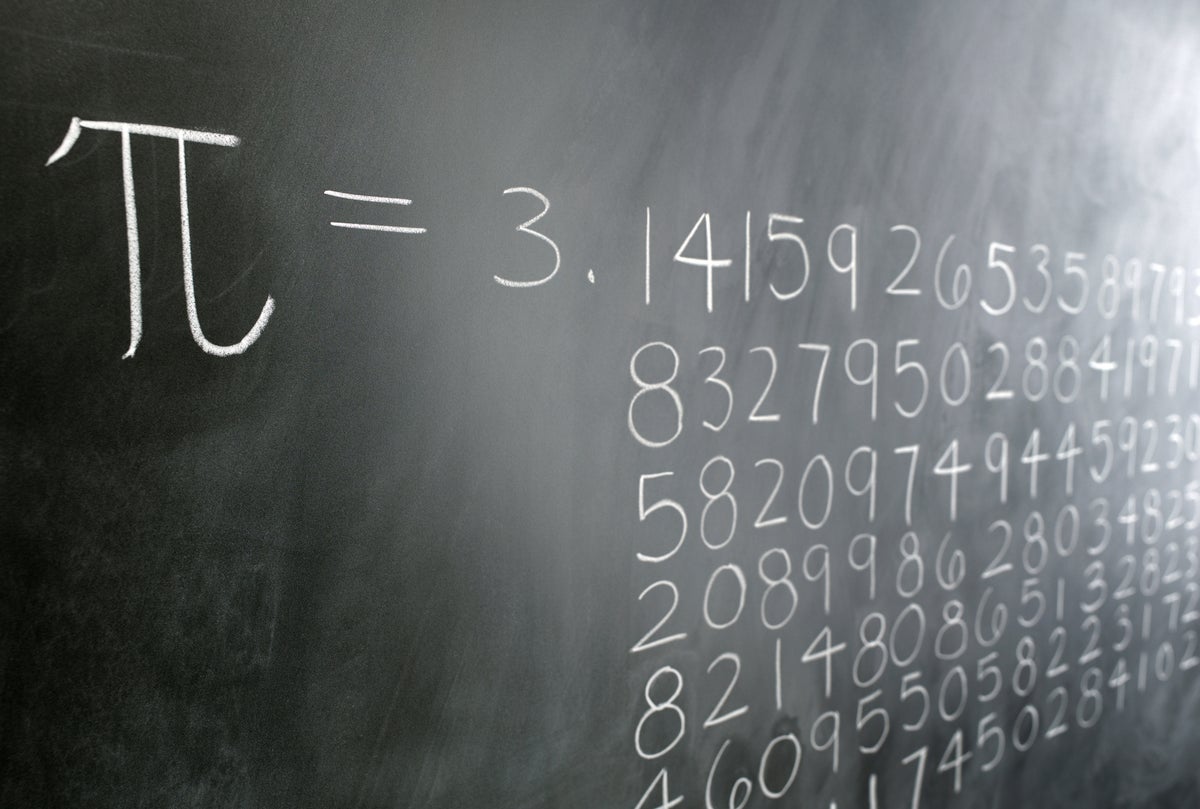
What Is Pi, and How Did It Originate?
Steven Bogart, a mathematics instructor at Georgia Perimeter College, answers
If still have question/s, please come back and ask.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,976
Do you know that a repeating decimal is a rational number?
Can you show that if [imath]R=.0824671\overline{671}\cdots[/imath] then [imath]R[/imath] is rational?
[imath][/imath][imath][/imath][imath][/imath]
Last edited by a moderator:
Unfortunately, PROVING that [imath]\pi[/imath] is not a rational number is a very hard proof. It took mathematicians over 2000 years to find it.
And proving that every number that has a decimal representation with an infinitely recurring string is a rational number is not exactly grade-school level
However, once you know that [imath]\pi[/imath] is not a rational number and that any number represented by a decimal with an infinitely recurring sequence is a rational number, it should be obvious that [imath]\pi[/imath] does not have an infinitely recurring sequence in its decimal representation.
And proving that every number that has a decimal representation with an infinitely recurring string is a rational number is not exactly grade-school level
However, once you know that [imath]\pi[/imath] is not a rational number and that any number represented by a decimal with an infinitely recurring sequence is a rational number, it should be obvious that [imath]\pi[/imath] does not have an infinitely recurring sequence in its decimal representation.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,686
Is it possible to have an infinite size consecutive sub-sequence of an infinite sized sequence? In other words, would it be possible to have:-
A={3,1,4,1,5...} with infinite digits
B=A+A+{some other infinite sequence of digits} where + means concatenate
, where B represents the digits of pi?
I'm probably going to get told that this suggestion is nonsense
A={3,1,4,1,5...} with infinite digits
B=A+A+{some other infinite sequence of digits} where + means concatenate
, where B represents the digits of pi?
I'm probably going to get told that this suggestion is nonsense
I think you are saying that something comes after infinity.Is it possible to have an infinite size consecutive sub-sequence of an infinite sized sequence? In other words, would it be possible to have:-
A={3,1,4,1,5...} with infinite digits
B=A+A+{some other infinite sequence of digits} where + means concatenate
, where B represents the digits of pi?
I'm probably going to get told that this suggestion is nonsense
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,686
Let me try to present a similar idea...
Imagine an infinite sequence of digits that make up some irrational number { x1,x2,x3,x4,.... }
Let n=1
Shift all elements of index≥n to the right and insert digit 3 at index n so that we have { 3, x1,x2,x3,x4... }
Shift all elements of index≥2n to the right and insert digit 3 at index 2n so that we have { 3, 3, x1,x2,x3,x4... }
Increment n
Shift all elements of index≥n to the right and insert digit 1 at n so that we have { 3,1, 3, x1,x2,x3,x4... }
Shift all elements of index≥2n to the right and insert digit 1 at 2n so that we have { 3,1, 3,1, x1,x2,x3,x4... }
Increment n
Shift all elements of index≥n to the right and insert digit 4 at n so that we have { 3,1,4, 3,1, x1,x2,x3,x4... }
Shift all elements of index≥2n to the right and insert digit 4 at 2n so that we have { 3,1,4, 3,1,4, x1,x2,x3,x4... }
Repeat this process, using digits of pi, until n=x
Who is to say that for some finite (but very large) value of x, this sequence of digits could never equal the actual sequence of pi's digits? I'd bet that such a proof/ disproof doesn't exist. In other words, I don't think that we can provide a definitive answer to the original post (which only requires this to be true for some finite value of x). However, it does seem massively unlikely.
And we could let x tend towards infinity. This would result in an irrational number that has an infinite-length repeat - but not periodic. This is obviously just a "thought experiment", but I find it quite interesting.
Last edited:
@Cubist
Real analysis is not something that I am expert in, but you are creating the sum of a rational and irrational number. I think that must be irrational.
[math]q, \ r \in \mathbb R, \ q \in \mathbb Q, \text { and } r \not \in \mathbb Q.\\ y = q + r.\\ \text {Assume, for purposes of contradiction, that } y \in \mathbb Q.\\ y + (-q) = r \implies r \in \mathbb Q \ \because \ \mathbb Q \text { is closed under addition.}\\ \text {But that conclusion contradicts the hypothesis that } r \not \in \mathbb Q.\\ \therefore \ y \not \in \mathbb Q.[/math]
I think that is a valid proof, but, as I said, real analysis is not my cup of tea.
Real analysis is not something that I am expert in, but you are creating the sum of a rational and irrational number. I think that must be irrational.
[math]q, \ r \in \mathbb R, \ q \in \mathbb Q, \text { and } r \not \in \mathbb Q.\\ y = q + r.\\ \text {Assume, for purposes of contradiction, that } y \in \mathbb Q.\\ y + (-q) = r \implies r \in \mathbb Q \ \because \ \mathbb Q \text { is closed under addition.}\\ \text {But that conclusion contradicts the hypothesis that } r \not \in \mathbb Q.\\ \therefore \ y \not \in \mathbb Q.[/math]
I think that is a valid proof, but, as I said, real analysis is not my cup of tea.
D
Deleted member 4993
Guest
Are you alleging that this is sloppy thinking because it was not stated explicitly?
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
No, I am not saying that this is sloppy thinking because it was not stated explicitly?
As I said, If JeffM was assuming that the sum of two rationals is in fact another rational, then the proof is fine.
On the other hand, if JeffM did not realized that the proof assumed that the sum of two rationals is a rational, then the proof has a flaw in it.
The reader of the proof will never know what JeffM was thinking.
JeffM even asked if the proof was valid and I gave my opinion.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
Then your proof was perfect!
D
Deleted member 4993
Guest
Next you will demand that we could not implicitly assume that sum of two even integers is even!!!!
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,561
SK,
JeffM asked if the proof was correct and I responded with what I thought was a nice suggestion.
Why are you being so hard on me? I guess that the corner is getting to you. You know that you should clean the corner occasionally to get rid of the spiderweb and your microwave food droppings.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,686
Thanks for engaging in a discussion
I agree with your proof.
I'm no expert on this topic either! You're very probably correct that an infinite sequence of digits couldn't be concatenated with itself. I just had the idea of having one (or more) infinite sequence of digits contained within an even bigger sequence of digits. A "higher degree" of infinity. I once saw a documentary about Cantor. But, I'm certainly no expert at this so I think I ought to stop posting about it at this point!
--
I then switched to thinking that an irrational number could have a single (but potentially large) set of repeated digits. Such a repeat couldn't be recurring since that would imply a rational number.
...could this perhaps be asking about a single repeat that happens after a "certain digit". @SirBuy doesn't specify what happens after this repeat, but I imagine that it would just be some continuation of an irrational sequence
...however this initial sentence does seem to imply that OP is asking if pi has a recurring repeat. Therefore I might have gone off topic here.
NOTE: I agree with all the posts above that state that pi has no recurring repetition of digits.