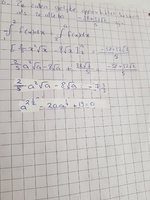Is it possible to solve this equation algebraically?

[Luna642]

I have to solve an equation algebraically, but I have no clue how to do that. Could someone please tell me how to solve it (without using a calculator)?
It's: x^2,5 - 20x^0,5 + 19 = 0

 

[Cubist]

It's: x^2,5 - 20x^0,5 + 19 = 0

You might need to re-check the above equation.

Is the following correct for f(x), which was perhaps given in an earlier part of the question?

[math] f(x)=\frac{x^2-4}{\sqrt{x}} [/math]

 

[Luna642]

Yes, that's the f(x) I was given.

You might need to re-check the above equation.

Is the following correct for f(x), which was perhaps given in an earlier part of the question?

[math] f(x)=\frac{x^2-4}{\sqrt{x}} [/math]

 

[Cubist]

Actually the mistake is in the final line of your image which appears as "a^2,5 - 2a*a^0,5 + 19 = 0
It looks like you might have copied this out and put an "a" instead of "0"

But the mistake is corrected when you write out "x^2,5 - 20x^0,5 + 19 = 0" in post #1 - I AGREE WITH THIS LINE

[math] a^{\frac{5}{2}} - 20\sqrt{a}+19=0 [/math]

 

[Cubist]

I would start with the substitution a=b² where b>0. This gives

[math] b^5-20b+19=0[/math]
can you spot any values of b that satisfy? If so then you've found a factor

 

[Luna642]

Yeah, I've tried that. It's obvious that 1 is one of the values, but how do you find the other one?

I would start with the substitution a=b² where b>0. This gives

[math] b^5-20b+19=0[/math]
can you spot any values of b that satisfy? If so then you've found a factor

 

[Cubist]

Yeah, I've tried that. It's obvious that 1 is one of the values, but how do you find the other one?

Cool. It would be helpful if you can post what you've already tried next time please.

I'll assume that you spotted b=1 is a solution, and you did the divide to obtain:-

[math] (b-1)(b^4+b^3+b^2+b-19)=0 [/math]
At this point we can answer "yes" to your original question since a quartic can be solved algebraically. I used a computer algebra system to do exactly this and the result is very unpleasant! A spreadsheet should accept this:-

=SQRT(15*POWER(5/18*SQRT(219705) + 875/54; 1/6)/(SQRT(-(-36*POWER(5/18*SQRT(219705) + 875/54; 2/3) + 15*POWER(5/18*SQRT(219705) + 875/54; 1/3) + 920))*2) - POWER(5/18*SQRT(219705) + 875/54; 1/3) + 230/(9*POWER(5/18*SQRT(219705) + 875/54; 1/3)) - 5/6)/2 - SQRT(-(-36*POWER(5/18*SQRT(219705) + 875/54; 2/3) + 15*POWER(5/18*SQRT(219705) + 875/54; 1/3) + 920))/(12*POWER(5/18*SQRT(219705) + 875/54; 1/6)) - 1/4

MUCH easier to graph it, or use Newton-Raphson to obtain b≈1.7341440448141308834652398764571. And don't forget to square "b" to obtain "a".

 

[Cubist]

...also worth pointing out that there's a -ve solution for b, and also a pair of complex conjugate solutions. But hopefully you're just considering the real solutions of "a"!

 

[firemath]

Per @Cubist's response, I was going to suggest graphing it, too. But since it seems that graphing calculators are prohibited, you would need to graph it by hand. Even though it might be a rather unpleasant venture (depending on your level of education), you'll be able to visualize the solution.

Also, in the last line, it looks like some one either has a squirrelly 0 or a term that needs to be combined. I believe Cubist already pointed out that it seemed like an error, but perhaps it needs to be a combined exponent instead.