Inverse Functions

[char]

I have the function (x-3)^2-16=y, but I can't figure out the inverse function. Please help me!!! Thanks in advance!

 

[Deleted member 4993]

I have the function (x-3)^2-16=y, but I can't figure out the inverse function. Please help me!!! Thanks in advance!

Switch "x" and "y" - then solve for "y".

 

[char]

I already know that, but I can't figure out how to solve for y.

 

[Deleted member 4993]

I already know that, but I can't figure out how to solve for y.

Show me how far you got and exactly where you are stuck.

 

[char]

(x-3)^2-16=x
(y-3)^2-16=x
y^2-9y-16=x
y^2-9y=x+16
y-3y=x+16
-4y=x+16
y=x-4

That's what I did but I don't know if its right???

 

[mmm4444bot]

(x-3)^2-16=x Don't switch just one variable; switch them both, at once.

(y-3)^2-16=x Yes, start with this line.

y^2-9y-16=x (y-3)^2 is not y^2 - 9y, but you don't want to square y - 3.

We have:

(y - 3)^2 - 16 = x

To solve for y, means to write y = something, not y^2 = something.

So, the next step is to take the square root of both sides.

Hint: Remember that the square root of (y - 3)^2 is not y - 3. It is |y - 3|.

 

[char]

Thanks so much for your help! Is this right??????

(x-3)^2-16=y switch y and x so
(y-3)^2-16=x
(y-3)^2-16+16=x+16
(y-3)^2=x+16
-sqrt(y-3+3)^2=-sqrt(x+16)+3

y=-sqrt(x+16)+3
or is it
y=sqrt(x+16)+3

Also another question is that a function or not? I'm totally confused as to what constitutes a function. All I can remeber is the vertical line test and I know that either answer is half of a parabola and passes the vertical line test.

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ (x-3)^2-16 \ is \ not \ 1 \ to \ 1, \ hence \ has \ no \ inverse.\)

\(\displaystyle f(-1) \ = \ f(7) \ = \ 0\)

 

[mmm4444bot]

Hi char:

Trying to learn about function inverses, while in a total state of confusion over the definition of a function, is tantamount to trying to find your way out of the middle of the forest without trail, map or guide.

Why would you do that?

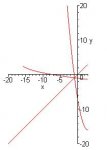
As Glenn pointed out, the given function y is not one-to-one. We need to split its domain at the vertex; then, y will be one-to-one in each half.

y[sup:2y151r22]-1[/sup:2y151r22] = 3 + sqrt(x + 16) over half of y's domain.

y[sup:2y151r22]-1[/sup:2y151r22] = 3 - sqrt(x + 16) over the other half.

Determining which half-domain belongs to each of these is easy, if you understand what inverse functions do (or the symmetry with y).

Use the graph below, or pick a test value for x, and reason it out!

I welcome specific questions.

Cheers ~ Mark

[attachment=0:2y151r22]inverse.JPG[/attachment:2y151r22]

 

[Denis]

(y-3)^2 - 16 = x
What's wrong with ye olde quadratic?
y^2 - 6y + 9 - 16 = x
y^2 - 6y - x - 7 = 0
y = 3 +- SQRT(x + 16)

 

[mmm4444bot]

What's wrong with ye olde quadratic [formula]?

Nothing, if that's what toots your scooter.

After checking the work in char post #3, I wanted to offer something with less steps because char is hurt'n.

 

[BigGlenntheHeavy]

\(\displaystyle Note, \ for \ what \ it \ is \ worth \ Dept: \ The \ sine \ and \ cosine \ haven't \ any \ inverses\)

\(\displaystyle \ ( \ they \ aren't \ 1 \ to \ 1 \ functions), \ unless \ we \ put \ a \ restriction \ on \ their \ domains, \ which \ we \ do.\)

\(\displaystyle No \ quadractic \ functions \ have \ an \ inverse \ unless \ we \ put \ a \ restriction \ on \ their \ domains,\)

\(\displaystyle usually \ at \ their \ axis \ of \ symmetry, \ as \ mmm4444bot \ pointed \ out.\)

 

[char]

Thanks for all of your help! You all rock!