inverse function

[calculusconfused]

i'm usually pretty good at these but this one has me stumped...

find the inverse function of:

f(x)=(e^(x)-e^(-x))/2

thanks ahead of time

 

[galactus]

This is an identity.

Note that \(\displaystyle sinh(x)=\frac{e^{x}-e^{-x}}{2}\)

 

[calculusconfused]

i have seen the identity, unfortunetly we have not reached that chapter yet and our teacher wants us to reach the answer the "old fashioned way"... that is by switching x and y and solving for y... i just don't know what step to take to get the answer....

 

[galactus]

Okey-doke then:

\(\displaystyle x=sinh(y)=\frac{e^{y}-e^{-y}}{2}\)

or \(\displaystyle e^{y}-2x-e^{-y}=0\)

Multiply through by \(\displaystyle e^{y}\):

\(\displaystyle e^{2y}-2xe^{y}-1=0\)

Now, apply the quadratic formula and discard the negative solution (because \(\displaystyle e^{y}>0\)).

Then, take the natural log of both sides. The solution should be an identity for \(\displaystyle sinh^{-1}(x)\)

 

[lookagain]

Post Deleted

Reason: I had typed in the wrong function to consider.

 

[galactus]

It would appear the poster is being asked to derive \(\displaystyle y=ln(x+\sqrt{x^{2}+1})=sinh^{-1}(x)\) from the given identity for sinh(x).

Noting the restriction on x such that \(\displaystyle y=sinh^{-1}(x) \;\ \text{is equivalent to} \;\ sinh(y)=x, \;\ \forall \;\ x,y\)

Using the quadratic formula, on can obtain \(\displaystyle e^{y}=x+\sqrt{x^{2}+1}\).

Upon taking the natural log of both sides gives:

\(\displaystyle y=ln(x+\sqrt{x^{2}+1})=sinh^{-1}(x)\)

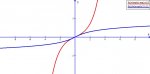
Here is the graph of \(\displaystyle \frac{e^{x}-e^{-x}}{2}\). It appears to pass the horizontal line test. A horizontal line only passes through it at most once.

Also, If g is the inverse function of f, then g(f(x))=x and f(g(y))=y. Both of these hold. Also, the function is increasing throughout its domain.

I am sorry, but it looks like it is one-to one to me.