Inverse Function

[Aladdin]

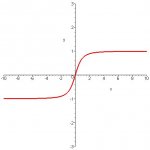
Given the function f defined by \(\displaystyle f(x) = \frac{x}{\sqrt{1+x^2}}\)

1) Show that f admits an inverse over R .

2) Determine the Domain of the inverse .

3) Express the inverse function .

Work :

A function admits an inverse in it's domain if it is continuous , defined and strictly monotonic .

f(x) is always cont. def. in R

f(x) can be written (x)(1+x^2)^-1/2

f'(x) = (x)(-1/2)(1+x^2)(2x) + (1)(1+x^2)^-1/2

f'(x) = (x^2)(1+x^2) + 1/sqrt{1+x^2)

f'(x) is always positive on R . So it's stricly increasing .

So f(x) admits an invers .

2) Domain of invers = range f(x)
R= ]-inf , +inf[
f^-1 = f(R) = ]f(-inf) , f(+inf)[ = ] ? , ? [

I think there's a trick to be done here . I've took x^2 as a common factor but still ....

3)f^-1 = ?
y=x/sqr{1+x^2}

y^2=x^2/1+x^2

y^2*(1+x^2) = x^2

y^2 + y^2*x^2 = x^2

y^2 = x^2(-y^2+1)

x^2= y^2/(-y^2+1)

x = +- y(/sqr{1}{-y^2+1) ....

Thanks in advance .

 

[daon]

The range of f will be (m, M), where m is the horizontal asymptote as x approaches -inf, M, similarly for x -> +inf. This works only in this case, and note they are open intervals as you showed the function is always monotonic.

 

[Aladdin]

The range of f will be (m, M), where m is the horizontal asymptote as x approaches -inf, M, similarly for x -> +inf. This works only in this case, and note they are open intervals as you showed the function is always monotonic.

Thank you doan , but what's the value of m & M .

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ y \ = \ \frac{x}{\sqrt(1+x^{2})}\)

\(\displaystyle Change: \ x \ = \ \frac{y}{\sqrt(1+y^{2})}\)

\(\displaystyle Ergo, \ x^{2} \ = \ \frac{y^{2}}{1+y^{2}}, \ \frac{1}{x^{2}} \ = \ \frac{1+y^{2}}{y^{2}}\)

\(\displaystyle \frac{1}{x^{2}} \ = \ \frac{1}{y^{2}}+1, \ \frac{1}{y^{2}} \ = \ \frac{1}{x^{2}}-1\)

\(\displaystyle \frac{1}{y^{2}} \ = \ \frac{1-x^{2}}{x^{2}}, \ y^{2} \ = \ \frac{x^{2}}{1-x^{2}}\)

\(\displaystyle y \ = \ f^{-1}(x) \ = \ \frac{x}{\sqrt(1-x^{2})}, \ -1 \ < \ x \ < \ 1\)

\(\displaystyle Check: \ f[f^{-1}(x)] \ = \ x \ = \ f^{-1}[f(x)], \ see \ graph \ below.\)

[attachment=0:222731xo]abc.jpg[/attachment:222731xo]

 

[Aladdin]

Thank you Gleen ...

Can you please , clarify number 2) for me .

Lim ( (x)/sqrt(1+x^2) as x tends to infinity ...

 

[BigGlenntheHeavy]

\(\displaystyle \lim_{x\to\infty}\frac{x}{\sqrt(1+x^{2})} \ = \ \lim_{x\to\infty} \frac{x}{\sqrt x^{2}} \ = \ \lim_{x\to\infty}\frac{x}{|x|}\)

\(\displaystyle = \ \lim_{x\to\infty}\frac{x}{x} \ = \ 1\)

\(\displaystyle Is \ this \ what \ you \ wanted?\)

 

[Aladdin]

\(\displaystyle \lim_{x\to\infty}\frac{x}{\sqrt(1+x^{2})} \ = \ \lim_{x\to\infty} \frac{x}{\sqrt x^{2}} \ = \ \lim_{x\to\infty}\frac{x}{|x|}\)

\(\displaystyle = \ \lim_{x\to\infty}\frac{x}{x} \ = \ 1\)

\(\displaystyle Is \ this \ what \ you \ wanted?\)

Yes ~ Thank you Gleen ...

Aha , So as x tends to -inf limit is -1

& as x tends to +inf limit is 1 .

 

[BigGlenntheHeavy]

\(\displaystyle Right, \ see \ below:\)

\(\displaystyle \lim_{x\to-\infty}\frac{x}{\sqrt(1+x^{2})} \ = \ \lim_{x\to-\infty}\frac{x}{\sqrt x^{2}}\)

\(\displaystyle = \ \lim_{x\to-\infty}\frac{x}{|x|} \ = \ \lim_{x\to-\infty}\frac{x}{-x} \ = \ -1\)

\(\displaystyle See \ graph \ below:\)

[attachment=0:x8yqqpjc]def.jpg[/attachment:x8yqqpjc]