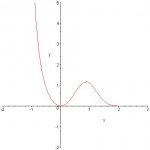
i need to find the inverse function of 3(x^2)(exp(-(x^3))) to solve part of my question
i first tried to split into 2 different functions, 3(x^2) and exp(-(x^3))) and find these inverses, (x/3)^(1/2) and
(-(log(x))^(1/3) and then recombined them, however this proved to be incorrect ( by checking an inverse graph image.)
i then tried to integrate the function to exp - (x^3) and then rearrange the integral, bearing in mind that y goes to yx when integrated.
I tried applying the natural log, ln in this case to simplify my rearranging however i was unable to do so.
any help or suggestions would be greatly appreciated as i have spent significant periods of time on this question to no avail.
I can easily check answers using graphs so all reasonable suggestions are welcome.
thank you very much.
i first tried to split into 2 different functions, 3(x^2) and exp(-(x^3))) and find these inverses, (x/3)^(1/2) and
(-(log(x))^(1/3) and then recombined them, however this proved to be incorrect ( by checking an inverse graph image.)
i then tried to integrate the function to exp - (x^3) and then rearrange the integral, bearing in mind that y goes to yx when integrated.
I tried applying the natural log, ln in this case to simplify my rearranging however i was unable to do so.
any help or suggestions would be greatly appreciated as i have spent significant periods of time on this question to no avail.
I can easily check answers using graphs so all reasonable suggestions are welcome.
thank you very much.