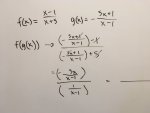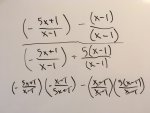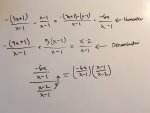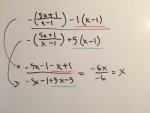Inverse Function: Solve for f(g(x))

[FritoTaco]

Hello everyone,

I'm unsure about solving for the inverse for the problem stated in my attachment file. It should be inversely related and result in x. So far, I think I'm cancelling out the right values but have 5x in there and I need to get rid of it. Can someone point me in the right direction, please?

 

[ksdhart2]

Well, the first thing I'd note is that your initial set-up is fine, but you've improperly cancelled several terms. You can see that these cancellations don't work by plugging in a random value for x, like, say, 3. Looking at just the numerator, we have, if your cancellation worked properly:

\(\displaystyle \displaystyle \left(-\frac{5x+1}{x-1}\right)-1=-\frac{5x}{x-1}\)

If we plug in x=3, let's see if the equality holds up.

\(\displaystyle \displaystyle \left(-\frac{5(3)+1}{(3)-1}\right)-1=-\frac{5(3)}{(3)-1}\)

\(\displaystyle \displaystyle \left(-\frac{16}{2}\right)-1=-\frac{15}{2}\)

\(\displaystyle \displaystyle \left(-8\right)-1=-\frac{15}{2}\)

\(\displaystyle \displaystyle -9=-\frac{15}{2}\)

Oops. So, clearly that cancellation was invalid. Instead, I'd return to the original problem and do the subtractions, recalling that you can write 1 as \(\displaystyle \dfrac{x-1}{x-1}\).

 

[FritoTaco]

Hey, I'm still confused about what you mean about doing the subtractions. I thought I did do that? Did I cancel out the wrong ones? Do I flip the denominator into the numerator?

 

[ksdhart2]

Oh, I'm sorry I was unclear before. I'll try explaining in a different way. What I meant was, if I was given a similar problem, let's say this one:

\(\displaystyle \displaystyle \frac{\left(-\frac{8x+7}{x-3}\right)-7}{\left(-\frac{8x+7}{x-3}\right)+8}\)

By "doing the subtraction," I meant to convert 7 and 8 to fractions. I know 7 can be written as 7 * 1, 8 can be written as 8 * 1, and 1 can be written as (x-3)/(x-3). Rewriting all of these things gives me:

\(\displaystyle \displaystyle \frac{\left(-\frac{8x+7}{x-3}\right)-\frac{7\left(x-3\right)}{\left(x-3\right)}}{\left(-\frac{8x+7}{x-3}\right)+\frac{8\left(x-3\right)}{\left(x-3\right)}}\)

Now, there's two fractions in the numerator, with a common denominator. There's also have two fractions in the denominator, with a common denominator. So, I'd just subtract straight across, in the usual fashion, and then simplify, combine like terms, and do general cleanup, as needed.

 

[FritoTaco]

For this problem, I tried flipping the denominator into numerator after your steps. I can't figure it out still, I end up with 5.

 

[Harry_the_cat]

For this problem, I tried flipping the denominator into numerator after your steps. I can't figure it out still, I end up with 5.

Simplify the numerator first (that's the bit above the big horizontal line (called the vinculum)):

\(\displaystyle \frac{-(5x+1)}{x-1} - \frac{x-1}{x-1} = \frac{-(5x+1)-(x-1)}{x-1} = \frac{-6x}{x-1}\)

Now do a similar thing to the denominator (below the vinculum).

THEN, do your reciprocating (ie change the division into multiplication).

Give it a go.

 

[Aido]

f(x)=1/x-5 and g(x)=7/x +5
How do i find (fog)(x) and (gof)(x)??

 

[FritoTaco]

Alright, after solving, my denominators were uneven again, should I get the common denominator again?

 

[Harry_the_cat]

Alright, after solving, my denominators were uneven again, should I get the common denominator again?

x-2 should just be -2, shouldn't it?

 

[Harry_the_cat]

f(x)=1/x-5 and g(x)=7/x +5
How do i find (fog)(x) and (gof)(x)??

This'll get lost in here. Start a new thread!
Have a go yourself first.

 

[Harry_the_cat]

Hey Frito,
With fractions, you need to get a common denominator only when adding or subtracting.

\(\displaystyle \frac{a}{b}+\frac{c}{d} =\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd}\)

You don't need a common denominator when multiplying or dividing.

\(\displaystyle \frac{a}{b} * \frac{c}{d} = \frac{ac}{bd}\)

 

[FritoTaco]

Wait, did I do it right, here? Edit: By the time I posted this, I just saw your last post. I'll have to look at it.