intervals

[ryan1015]

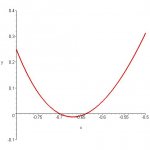
let g(x)=5x^4 +6x +3 a) find the intervals on which g is increasing and decreasing. b) find the intervals of concavity and the inflection points.


i know first derivative will show intervals of increase?decrease and 2nd derivative shows concavity and inflection points. my first derivative was 20x^3+6 and my 2nd derivative was 60x. i believe i set the first derivative to zero to get intervals of decrease and the same for 2nd derivative but i dont really know

 

[tkhunny]

What is ti that you are not knowing? You have given a complete description. Why not just finish up and be done? No need to doubt.

g(x) = 0 gives solutions or the equation or roots of g(x).

g'(x) = 0 gives potential min or max. Solve 20x^3 + 6 = 0 to find such points. The slope is positive or negative on each side. It may or may not change at the point.

g"(x) = 0 gives potential points of inflection. The concavity is positive or negative on each side. It may or may not change at the point. A point oi inflection will supersede a potential min or max.

Okay, now do it.

 

[BigGlenntheHeavy]

$\displaystyle g(x) \ = \ 5x^{4}+6x+3$

$\displaystyle g'(x) \ = \ 20x^{3}+6 \ = \ 0, \ x \ \dot= \ -.67$

$\displaystyle g(-.67) \ \dot= \ -.012$

$\displaystyle g"(x) \ = \ 60x^{2}, \ g"(-.67) \ > \ 0, \ rel. \ min.$

$\displaystyle g"(x) \ = \ 60x^{2} \ = \ 0, \ x \ = \ 0$

$\displaystyle Hence, \ (0,3) \ possible \ point \ of \ inflection, \ g"(-1) \ > \ 0 \ and \ g"(1) \ > \ 0, \ ergo, \ no \ inflection \ point.$

$\displaystyle Therefore, \ summing \ up, \ decreasing \ on \ (-\infty,-.67] \ and \ increasing \ on \ [-.67,\infty), \ has \ a \ absolute$

$\displaystyle \ min. \ at \ (-.67,-.012), \ and \ no \ points \ of \ inflection, \ and \ is \ concave \ up \ throughout.$

$\displaystyle See \ plot.$

[attachment=0:27gpwrku]def.jpg[/attachment:27gpwrku]