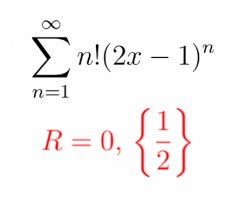You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Interval of Convergence
- Thread starter I Love Pi
- Start date
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
In calculating p you replaced (n+1) with1 + 1/n. Can you justify that step?
(-2)^n is an alternating series with the terms getting larger and larger. The difference between two consecutive terms is growing without bound. That along with n! growing w/o bound should tell you that n!(-2)^n is not convergent.
Just calculate the p value correctly and be done.
(-2)^n is an alternating series with the terms getting larger and larger. The difference between two consecutive terms is growing without bound. That along with n! growing w/o bound should tell you that n!(-2)^n is not convergent.
Just calculate the p value correctly and be done.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
You have multiple answers! You wrote that |2x-1|*oo = oo. This is not true! If x = 1/2, then |2x-1|=0. 0*(something approaching infinity) does not equal infinity, it equal 0! Just like you said at some point.This was very helpful. I have attached my revised solution. Please let me know if this is what you meant. Thank you, again!
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Yes, but who said that p diverges for all values of x.My solutions manual says the point of convergence is {1/2}. If p diverges as you suggest, then wouldn’t this conflict with the solutions manual?