Scrutinize
Junior Member
- Joined
- Sep 16, 2019
- Messages
- 52
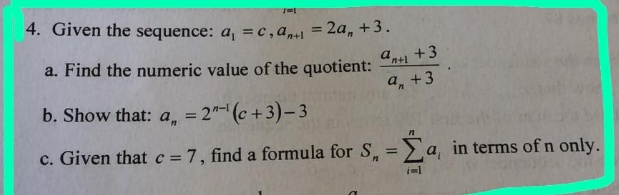
Gyazo
I know how to do the first part, I substituted an+1 and got 2 for the answer (Which is correct)
This question is a geometric and arithmetic sequence, and I'm not sure how to do part b and c. I tried using both arithmetic and geometric equations to see if i can see a similarity and work of that but I can't find anything. On the test just to note, I'll only have arithmetic and geometric rules, so for whoever helps me please keep that in mind so that you know that I can only work of arithmetic and geometric rules.
Thank you so much! Any help would be very helpful.
