interesting problem

[dynamo]

just need to verify this.
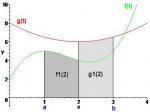
if a have a function f(x) and a function g(x) and the area under f(x)
from a known a to a variable x is (integral from a to x of)f(x);
let f1(x)= (integral from a to x of)f(x);
and
the area under g(x) from the same variable x to a known b is
(integral from x to b of)g(x)
let g1(x)=(integral from x to b of)g(x);
now let c(x)= f1(x)+g1(x);
first isnt c the area of the two regions
and isnt
c'(x)(the derivative of c) the function of the curve above the two
regions(i.e region under f1(x) and region under g1(x))
between a and b?
Or at least if the function of the curve above the two
regions(i.e region under f1(x) and region under g1(x))
is fn(x)
isnt fn(b)=c'(b);
by second fundamental theorem of calculus
would be greatful for any reply.thanks

 

[mmm4444bot]

let f1(x)= (integral from a to x of)f(x);
and
let g1(x)=(integral from x to b of)g(x);

If f1 and g1 are supposed to be functions for area underneath f and g, respectively, then you're going to have difficulty using the same independent variable for all four functions.

I'm thinking that you mean the following, instead.

f(t) and g(t) are continuous functions on the interval [a, b].

f1(x) and g1(x) are functions for the area underneath f(t) and g(t), respectively.

\(\displaystyle f1(x) \;=\; \int^x_a f(t) \, dt\)

\(\displaystyle g1(x) \;=\; \int^b_x g(t) \, dt\)

where x is a value that varies between the endpoints of the interval [a, b].

EG:

\(\displaystyle f(t) \;=\; t^3 \;-\; 5t^2 \;+\; 7t \;+\; 2\)

\(\displaystyle g(t) \;=\; \frac{1}{2}t^2 \;-\; 2t \;+\; 8\)

Let a = 1 and b = 3

\(\displaystyle f1(x) \;=\; \int^x_1 f(t) \, dt\)

\(\displaystyle g1(x) \;=\; \int^3_x g(t) \, dt\)

\(\displaystyle 1 < x < 3\)

Let x = 2

f1(2) will be the area underneath f(t) from x = 1 to x = 2 (the darker grey region below)

g1(2) will be the area underneath g(t) from x = 2 to x = 3 (the lighter grey region below)

[attachment=0:1v6n7dvc]Curves.JPG[/attachment:1v6n7dvc]

Does this scenario jive with what you're thinking?

 

[dynamo]

thanks for replying.precisely,only that the two curves touch at x so it forms a continuous curve.Then i want to get the equation of the curve formed by the concatenation of the two curves (and i dont want to use piecewise functions) i've changed the question a little now.It now looks like this

if a have a function f(x) and a function g(x) and the area under f(x)
from a known a to a known b is (integral from a to b)f(x);
let f1(x)= (integral from a to b)f(x);
and
the area under g(x) from a known b to c is
(integral from b to c)g(x)
let g1(x)=(integral from b to c)g(x);
now let A(x)= f1(x)+g1(x);


//things are clear up to this point

the second fundamental theorem of calculus seems
to tell me
that since
A(x)=(integral from a to c)fn(x)dx;//where fn(x) is the function i'm
trying to get
A'(c)=fn(c);
substituting x for c should give
A'(x)=fn(x);

isnt
fn(x) the function of the curve above the two
regions(i.e region under f1(x) and region under g1(x))