Sweatyapples
New member
- Joined
- Feb 7, 2015
- Messages
- 10
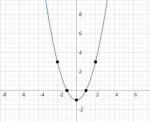
Find the volume generated when the area bounded by y = x^2 -1 and the x-axis is rotated about:
a) the x-axis
b) the y-axis
a) V = π ∫ {1, -1} (x^2 -1)^2 dx
= π ∫ {1, -1} (x^4 - 2x^2 + 1) dx
= π [((1/5)(1)^5 -(2/3)(1)^3 + 1) - ((1/5)(-1)^5 - (2/3)(-1)^3 -1))]
= (16π/15)u^3
b) y = x^2 -1
x^2 = y + 1
V = π ∫ {b, a} (y + 1) dy
V = π ∫ {b, a} (y + 1) dy
I'm just confused on the limits regarding (b), I've tried a number of different limits however I cannot seem to generate the correct answer (which is pie/3 according to my book).
a) the x-axis
b) the y-axis
a) V = π ∫ {1, -1} (x^2 -1)^2 dx
= π ∫ {1, -1} (x^4 - 2x^2 + 1) dx
= π [((1/5)(1)^5 -(2/3)(1)^3 + 1) - ((1/5)(-1)^5 - (2/3)(-1)^3 -1))]
= (16π/15)u^3
b) y = x^2 -1
x^2 = y + 1
V = π ∫ {b, a} (y + 1) dy
V = π ∫ {b, a} (y + 1) dy
I'm just confused on the limits regarding (b), I've tried a number of different limits however I cannot seem to generate the correct answer (which is pie/3 according to my book).