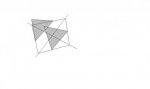
Integration (square with vertical slice of equilateral triangles)

[ZyzzBrah]

Solution:
\(\displaystyle A_{square} = (\sqrt{x^2+y^2})^2\)

\(\displaystyle V = \int_{-y}^{y} A dx\)

\(\displaystyle V = \int_{-y}^{y} {x^2+y^2} dx \)

\(\displaystyle V = 2y^3\) Ans

wait somethings wrong didnt notice the equilateral
gonna redo it for a sec

 

[Deleted member 4993]

View attachment 1553
Solution:
\(\displaystyle A_{square} = (\sqrt{x^2+y^2})^2\)

\(\displaystyle V = \int_{-y}^{y} A dx\)

\(\displaystyle V = \int_{-y}^{y} {x^2+y^2} dx \)

\(\displaystyle V = 2y^3\) Ans

wait somethings wrong didnt notice the equilateral
gonna redo it for a sec

http://www.freemathhelp.com/forum/forum.php

• 
  
  
  
  
  
  As stated - since the size of the square is not given - the magnitude of the volume can be any thing.

 

[ZyzzBrah]

can you check if my solution is correct?

coordinates are:
(0,y0), (x0,0),(0,-y0),(-x0,0)

and x0 = y0 since its a square

\(\displaystyle A_{triangle} = \frac{s^{2}\sqrt{3}}{4}\)
Then the integral should be
\(\displaystyle \int_{-y_o}^{y_o} A_{triangle} dx \)

to solve for s:
s = right - left

right line:
\(\displaystyle y = -\frac{y_{o}}{x_{o}}(x-x_{o})\)

left line:
\(\displaystyle y = \frac{y_{o}}{x_{o}}(x-x_{o})\)

\(\displaystyle s = -\frac{y_{o}}{x_{o}}(x-x_{o}) - (\frac{y_{o}}{x_{o}}(x-x_{o}))\)

\(\displaystyle s = -2\frac{y_{o}}{x_{o}}(x)\)

getting back to the integral
\(\displaystyle V = \int_{-y_o}^{y_o} \frac{s^{2}\sqrt{3}}{4} dx \)

\(\displaystyle V = \int_{-y_o}^{y_o} \frac{(-2\frac{y_{o}}{x_{o}}(x))^{2}\sqrt{3}}{4} dx \)

\(\displaystyle V = \sqrt{3}(\frac{y_o}{x_o})^{2} \int_{-y_o}^{y_o} x^2 dx \)

yo = xo

\(\displaystyle V = \frac{\sqrt{3}}{3} (x^3)_{-y_{o}}^{y_{o}} \)

\(\displaystyle V = \frac{2\sqrt{3}}{3} * {y_o}^3 \)

 

[galactus]

I bet that should say "unit square".

This being the case, we can find the right half and double the answer.

Since it is a unit square with vertices on the axes (like a diamond), then x goes from

0 to \(\displaystyle \frac{1}{\sqrt{2}}\).

So, the base of the slice is then \(\displaystyle 2(\frac{1}{\sqrt{2}}-x)\)

The area of the slice is then \(\displaystyle \frac{\sqrt{3}}{4}(2(\frac{1}{\sqrt{2}}-x))^{2}\)

So, we have \(\displaystyle \displaystyle \frac{\sqrt{3}}{2}\int_{0}^{\frac{1}{\sqrt{2}}}(\sqrt{2}-2x)^{2}dx=\frac{1}{\sqrt{6}}\)

 

[ZyzzBrah]

brilliant solution galactus
we have the same approach but you assumed it as unity

anyway is my approach (3rd post) acceptable?

 

[galactus]

anyway is my approach (3rd post) acceptable?

Since the side length of the square is 'a', then x varies from 0 to \(\displaystyle \frac{a}{\sqrt{2}}\)

Which would give \(\displaystyle \displaystyle 2\cdot \frac{\sqrt{3}}{4}\int_{0}^{\frac{a}{\sqrt{2}}}\left(2(\frac{a}{\sqrt{2}}-x)\right)^{2}dx=\frac{a^{3}}{\sqrt{6}}\)

It would appear we're off by a factor of \(\displaystyle 2\sqrt{2}\). That is, your answer multiplied by

\(\displaystyle \frac{1}{2\sqrt{2}}\) gives my answer.

\(\displaystyle \frac{2}{\sqrt{3}}\cdot \frac{1}{2\sqrt{2}}=\frac{1}{\sqrt{6}}\)

When you simplified, you should have gotten \(\displaystyle \frac{-y_{0}}{x_{0}}(x-x_{0})-\frac{y_{0}}{x_{0}}(x-x_{0})=\frac{-2(x-x_{0})y_{0}}{x_{0}}\)

But, you have \(\displaystyle -2\cdot \frac{y_{0}}{x_{0}}x\)

My solution is different from yours. But, then again, I may be in error. Seems logical, though.


I edited my first post because I had forgotten to multiply by 2.