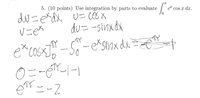Integration by parts
- Thread starter Kcashew
- Start date
- Joined
- Nov 24, 2012
- Messages
- 3,021
I would set:
[MATH]I=\int_0^{\pi} e^x\cos(x)\,dx[/MATH]
Using your substitutions, we obtain:
[MATH]I=\left[e^x\cos(x)\right]_0^{\pi}+\int_0^{\pi}e^x\sin(x)\,dx[/MATH]
[MATH]I=-(e^{\pi}+1)+\int_0^{\pi}e^x\sin(x)\,dx[/MATH]
Now, try IBP again on the remaining integral:
[MATH]u=\sin(x)\implies du=\cos(x)\,dx[/MATH]
[MATH]dv=e^x\,dx\implies v=e^x[/MATH]
[MATH]I=-(e^{\pi}+1)+\left(\left[e^x\sin(x)\right]_0^{\pi}-\int_0^{\pi} e^x\cos(x)\,dx\right)[/MATH]
Can you proceed?
[MATH]I=\int_0^{\pi} e^x\cos(x)\,dx[/MATH]
Using your substitutions, we obtain:
[MATH]I=\left[e^x\cos(x)\right]_0^{\pi}+\int_0^{\pi}e^x\sin(x)\,dx[/MATH]
[MATH]I=-(e^{\pi}+1)+\int_0^{\pi}e^x\sin(x)\,dx[/MATH]
Now, try IBP again on the remaining integral:
[MATH]u=\sin(x)\implies du=\cos(x)\,dx[/MATH]
[MATH]dv=e^x\,dx\implies v=e^x[/MATH]
[MATH]I=-(e^{\pi}+1)+\left(\left[e^x\sin(x)\right]_0^{\pi}-\int_0^{\pi} e^x\cos(x)\,dx\right)[/MATH]
Can you proceed?
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
In my opinion you gave no answer. An answer, in my opinion, should be in the form of \(\displaystyle \int_0^\pi e^xcos(x)dx = .... = ....=...= your \ answer.\)
The answer to a definite integral is a real number, not an equation.
You wrote that the answer was \(\displaystyle e^\pi = -2\). First of that is an equation. 2nd of all, e\(\displaystyle \approx\) 2.718 and \(\displaystyle \pi\approx 3.141592654\). How can you raise a positive number like e to any power and get a negative answer.
Seriously, you need to get a better sense of numbers and know that an indefinite integral equals a function and that an indefinite integral equals an area which is expressed in square units.
Someone just asked this exact question. You can view it by going to this post.
Thank you very much for your time in helping me solve this problem. The solution I came up with is this:
-(e^pi + 1)/2
- Joined
- Nov 24, 2012
- Messages
- 3,021
