I've got this arclength problem

And I did the first bits with the arclength formula (
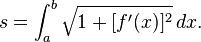 )
)
until I reach a bit where I have Integration from 9 to 1 of Sqrt(.25y+.25y^-1 -.5)
I don't know how to integrate that. U substitution fails because .25y^-1 turns into -.25y^-2 in the Du.
I do know from using a computer that I'm on the right track as the area under that curve from 9 to 1 was the correct answer, and that the answer is 10.66667

And I did the first bits with the arclength formula (
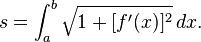
until I reach a bit where I have Integration from 9 to 1 of Sqrt(.25y+.25y^-1 -.5)
I don't know how to integrate that. U substitution fails because .25y^-1 turns into -.25y^-2 in the Du.
I do know from using a computer that I'm on the right track as the area under that curve from 9 to 1 was the correct answer, and that the answer is 10.66667
