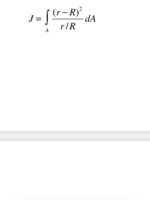Integrating with respect to lower bound
- Thread starter sepoto
- Start date
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
That looks like the pretty standard "indefinite integral" where the "A" subscript indicates that the integral function is to be written in terms of the variable "A". For example \(\displaystyle \int_A A^2 dA= \frac{1}{3}A^3+ C\).
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,690
HallsofIvy could be right.
I have also seen this type of notation in a mechanics context where it can mean integrate a function over an area(A), or surface(S), etc. Often it will be accompanied by a diagram indicating the region that A actually covers.
The f that you posted could be in terms of polar coordinates since it uses "r". This is how to integrate a function f over a circular area of radious "R" in polar coordinates...
[math]\int_{0}^{2\pi} \int_{0}^{R} f\cdot r\,dr\,d\theta[/math]
So in your case it might end up as...
[math] \int_{0}^{2\pi} \int_{0}^{R} \frac{\left(r-R\right)^2}{\left(\frac{r}{R}\right)} \cdot r\,dr\,d\theta [/math]
...but it really depends on the context and any information there is concerning "A".
I have also seen this type of notation in a mechanics context where it can mean integrate a function over an area(A), or surface(S), etc. Often it will be accompanied by a diagram indicating the region that A actually covers.
The f that you posted could be in terms of polar coordinates since it uses "r". This is how to integrate a function f over a circular area of radious "R" in polar coordinates...
[math]\int_{0}^{2\pi} \int_{0}^{R} f\cdot r\,dr\,d\theta[/math]
So in your case it might end up as...
[math] \int_{0}^{2\pi} \int_{0}^{R} \frac{\left(r-R\right)^2}{\left(\frac{r}{R}\right)} \cdot r\,dr\,d\theta [/math]
...but it really depends on the context and any information there is concerning "A".
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,750
The context would help. Can you show us the definitions of the variables (especially of A), and anything else that is said about it?
It looks to me like a definite integral, likely over a region A, since it is assigned to a variable (and therefore ought to represent a number). On the other hand, then A would be a fixed region, and I am not happy also using dA in the same integral. More typically, as here, they would have different names.
It looks to me like a definite integral, likely over a region A, since it is assigned to a variable (and therefore ought to represent a number). On the other hand, then A would be a fixed region, and I am not happy also using dA in the same integral. More typically, as here, they would have different names.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,690
Thanks for posting the extra info.
It seems to me, from the diagrams, that R is the radius of the centre of the beam. So the inner radius would be R-h/2, and the outer is R+h/2. So I think the text you wrote might be wrong about the definition of r and R.
Perhaps the region to integrate over, "A" is the area shown in the top picture. I think this is likely because the top diagram considers a small section of the arch, dφ. But also it could be the bottom picture, since you wrote "A is defined as the cross sectional area of an arch beam" and the bottom image is a cross section.
It seems very confusing to me. Perhaps not a very clear (or correct) book! It might help if you could post more of the surrounding text - assuming that you still want to get to the bottom of this particular integral.
It seems to me, from the diagrams, that R is the radius of the centre of the beam. So the inner radius would be R-h/2, and the outer is R+h/2. So I think the text you wrote might be wrong about the definition of r and R.
Perhaps the region to integrate over, "A" is the area shown in the top picture. I think this is likely because the top diagram considers a small section of the arch, dφ. But also it could be the bottom picture, since you wrote "A is defined as the cross sectional area of an arch beam" and the bottom image is a cross section.
It seems very confusing to me. Perhaps not a very clear (or correct) book! It might help if you could post more of the surrounding text - assuming that you still want to get to the bottom of this particular integral.
In McGrawHill Mechanics of materials it’s described in more detail how the integral is solved by converting to a function including “ln”.
The integral for J I first posted seems to be just a fancy embellishment which is shorthand and I was supposed to know that somehow. Attached is from the chapter on bending.
The integral for J I first posted seems to be just a fancy embellishment which is shorthand and I was supposed to know that somehow. Attached is from the chapter on bending.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,690
This new image uses the symbol A in three different contexts:-
- as a single point location (in the diagrams)
- as a defined, static, area
- as "dA" meaning "with respect to area"
)
Last edited:
The letter R is used twice and means two different things. Some of the language in McGraw is a broken English but I could follow that integral respect to dA is symbolic and enumerates to some definite integrals. Sometimes it seems these texts are written a way that no one should understand them. Thanks for your posts.